论文解读:Leave No Context Behind Efficient Infinite Context Transformers with Infini-attention
本文最后更新于 2024年9月5日 晚上
Google在今年4月份发布了一篇论文《Leave No Context Behind: Efficient Infinite Context Transformers with Infini-attention》,光看这篇论文标题就很吸引人,既是“No Context Behind”又是“Infini-attention”,那让我们看看Infini-Transformers是否能够真的做到无限上下文的处理。
1. Background
- 传统注意力机制
Infini — Transformers和大部分魔改注意力机制模型的目的一样,都是为了解决长文本处理的问题。传统Transformers的注意力机制在内存占用和计算时间上都呈现平方复杂度,因此在处理超长文本时会遇到困难。
- 记忆压缩
为了处理超长文本,以往的一些记忆压缩方法通过将序列信息压缩到一个固定大小的隐状态中,其代表就是RNN模型。这种方法有着较高的计算效率,但是很难将整个上下文信息存储到单个固定大小的向量中。因此需要找到一种能够平衡简单性与压缩性能的方法。
- Transformer-XL
Transformer-XL针对长文本进行了优化,以固定长度的序列片段作为输入,并会将上一阶段缓存的状态用于当前阶段的注意力计算,如下图:
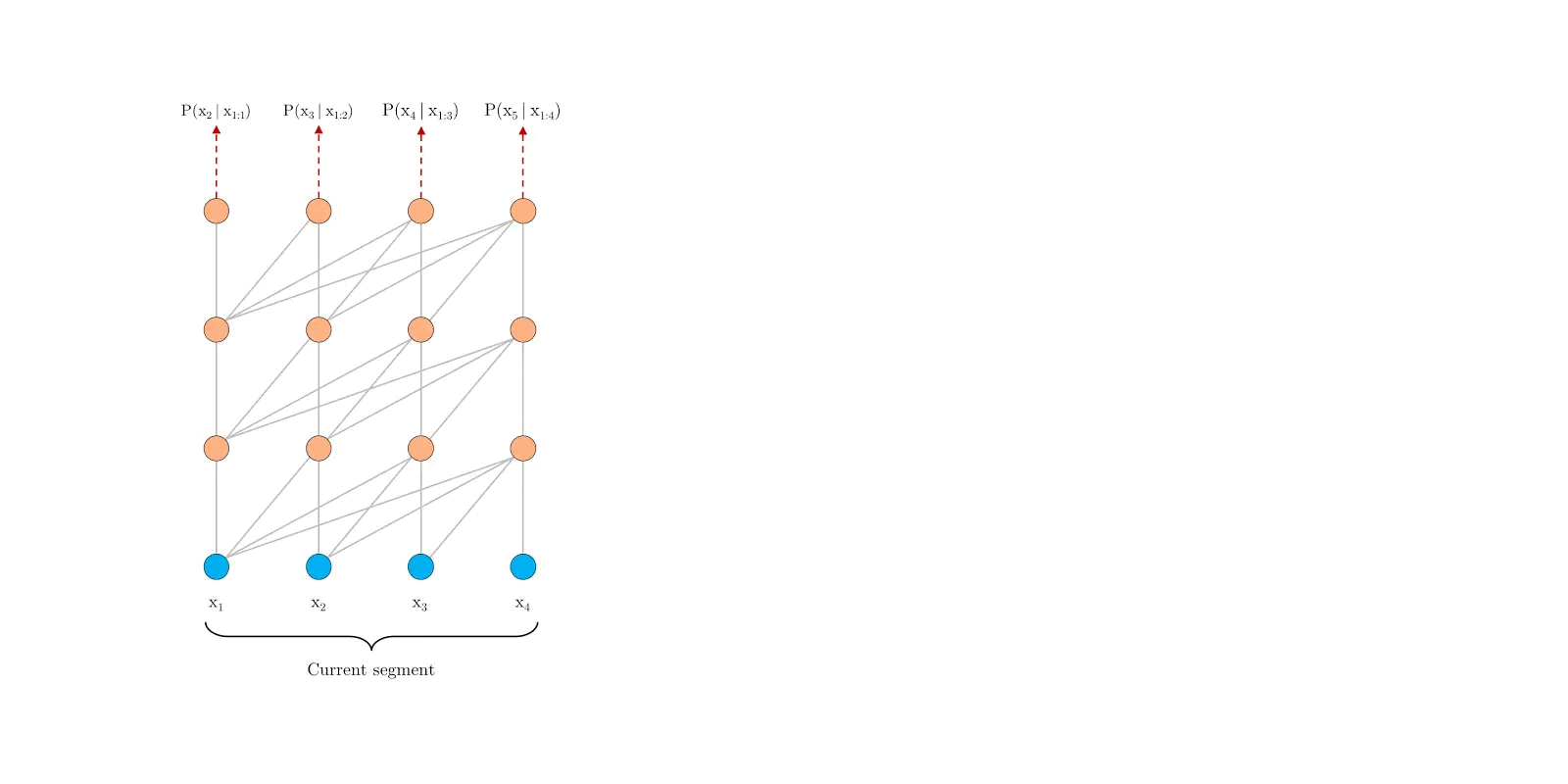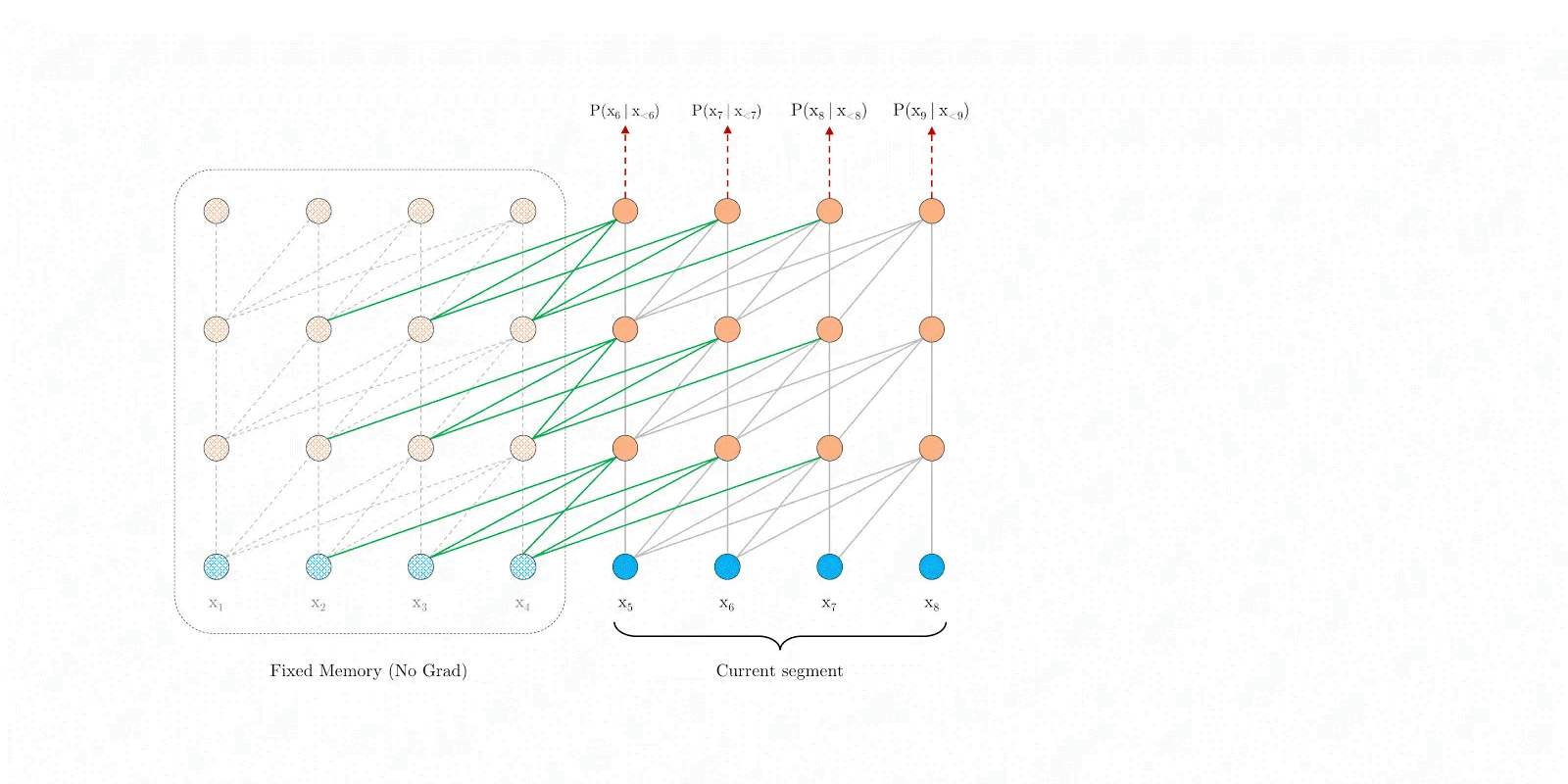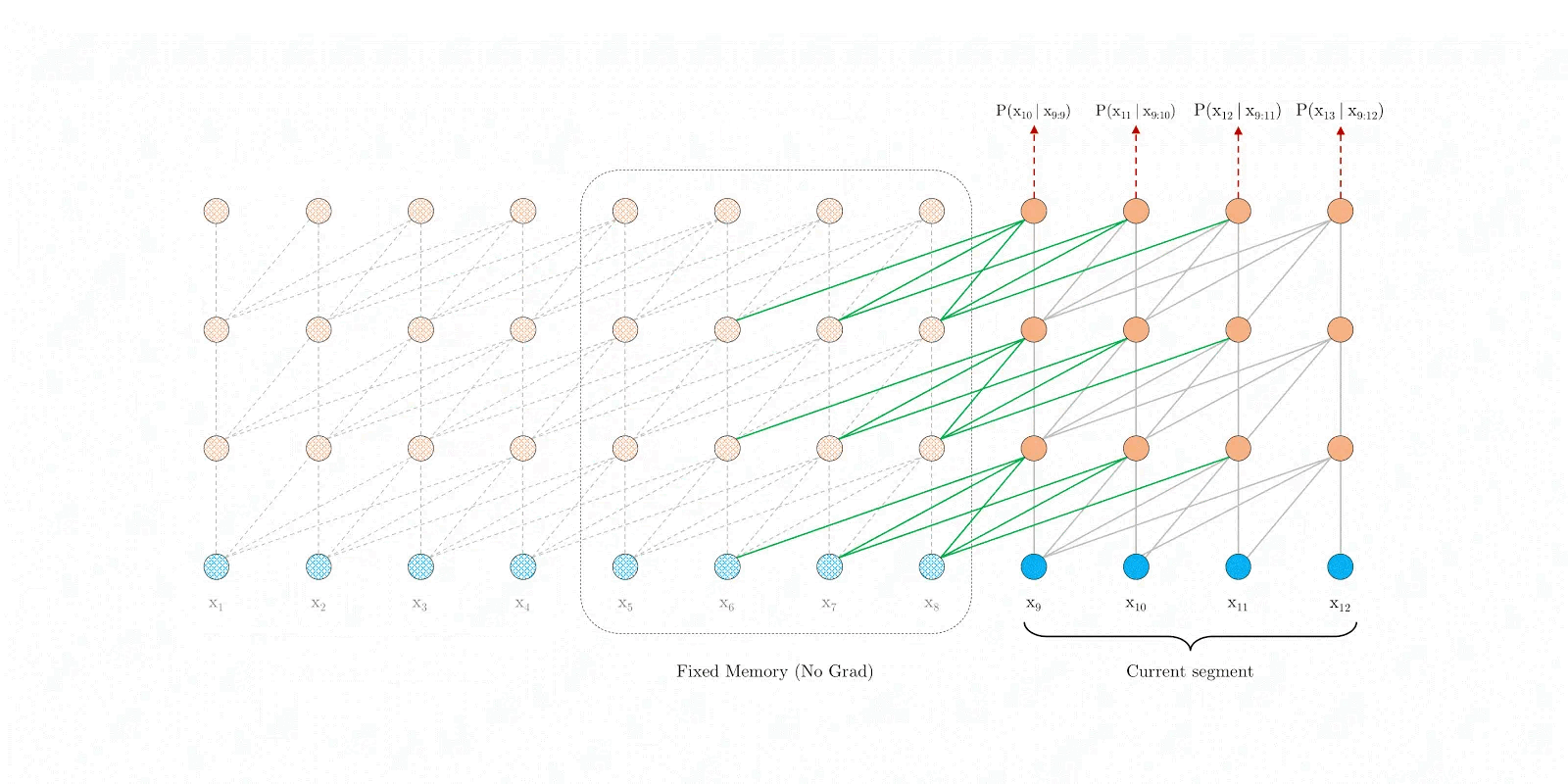
通过序列分段和缓存状态,Transformer-XL可以处理更长的文本,Infinit-attention也是使用了这种思想,但是在状态缓存策略上有所不同。
2. Infini-attention
2.1 Infini-attention = Local Attention + RNN
如下图所示,为了能有效处理长序列,Infini-Transformer采取了与Transformer-XL相似的策略,将长序列分割为固定长度的片段,并计算每个片段的Causal scaled dot-product attention,但是这种注意力仅局限在当前的片段中,并不能利用全局的上下文信息。为此,Infini-Transformer引入了一个Compressive memory模块,用于存储全局的上下文信息。在计算当前片段的注意力输出时,会将全局的上下文信息与当前片段的局部信息进行融合,然后更新全局的上下文信息。这种机制非常类似于RNN模型,因此Infini-attention可以看作是Local Attention和RNN的结合。
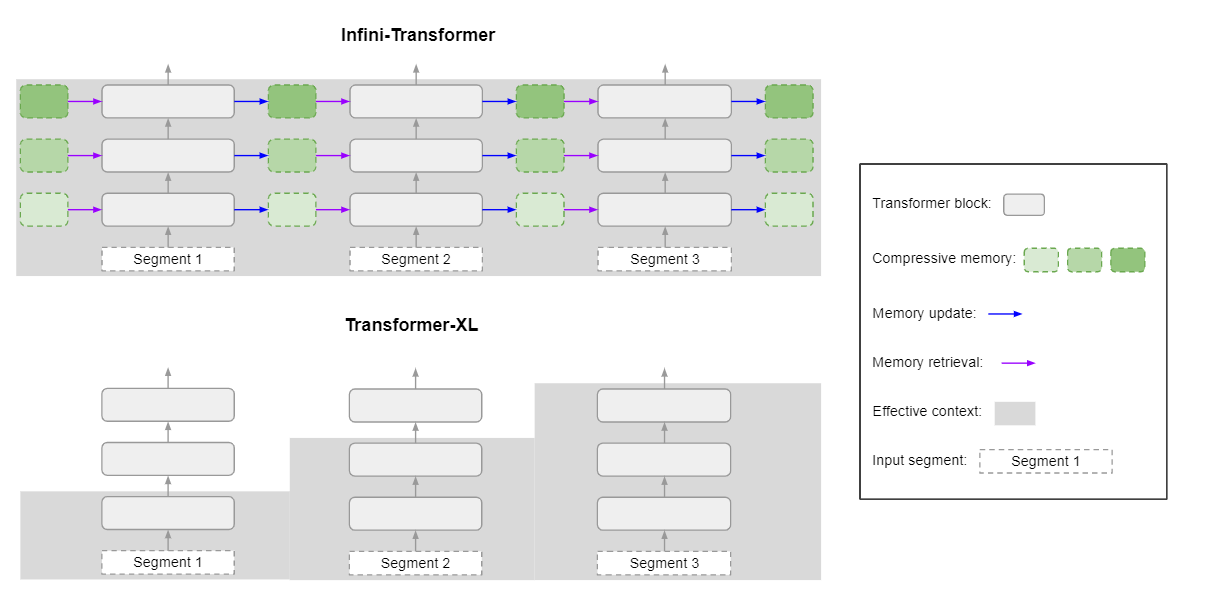
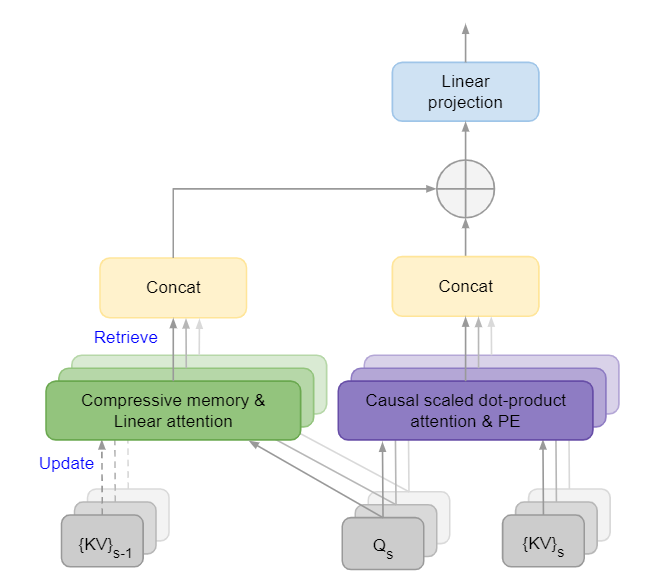
Infini-attention的整体框架如下图所示,\(\{KV\}_{s-1}\)和\(\{KV\}_{s}\)分别表示上一片段和当前片段的key和value,\(Q_s\)表示当前阶片段的query,PE表示位置编码,图中Causal scaled dot-product attention就是普通的Transformer的注意力计算,而对于Compressive memory的处理包括Retrieve和Update两个步骤:
- Retrieve是利用当前的query去检索压缩记忆中的有效信息,并将其融合到Local Attention的输出中,这样得到的最终输出理论上包含了全局上下文信息。
- Update是将当前片段的\(KV\)信息更新到压缩记忆中,以便下一阶段的注意力计算。Updata是在Retrieve之后进行的。
与RNN相似,Infini-attention维护一个循环的记忆状态以有效地跟踪全局上下文信息,我们可以用以下函数表示: \[ O_s,M_s=\text{infini-attention}(X_s,M_{s-1}) \]
2.2 Scaled Dot-product Attention
对于多头注意力的每个头,先以片段序列\(X \in \mathbb{R}^{L \times d_{model}}\)为输入,计算query、key和value: \[ Q=XW_Q,K=XW_K,V=XW_V \] 其中\(W_Q \in \mathbb{R}^{d_{model} \times d_k},W_K \in \mathbb{R}^{d_{model} \times d_k},W_V \in \mathbb{R}^{d_{model} \times d_v}\)是可训练的投影矩阵,\(d_k,d_k,d_v\)分别是query、key和value的维度。然后计算注意力输出: \[ A_{dot}=\mathrm{softmax}\left(\frac{QK^{T}}{\sqrt{d_{k}}}\right)V. \]
2.3 Compressive Memory
Compressive Memory是Infini-attention的核心模块,用于存储全局的上下文信息。其运行机制包括Memory Retrieve、Long-term context injection和Memory Update三个步骤。
2.3.1 Memory Retrieve
为了检索压缩记忆中的有效信息,Infini-attention使用当前片段的query \(Q \in \mathbb{R}^{N \times d_{key}}\)去检索记忆\(M_{s-1}\in\mathbb{R}^{d_{key}\times d_{value}}\),得到检索结果\(A_{mem}\in\mathbb{R}^{N \times d_{value}}\): \[ A_{mem}=\frac{\sigma(Q)M_{s-1}}{\sigma(Q)z_{s-1}}. \] 其中\(\sigma\)是激活函数,原文中使用的是\(\text{ELU}+1\),\(z_{s-1}\)是归一化因子,非线性和归一化因子的引入是为了是训练更为稳定。
2.3.2 Long-term context injection
为了使最后的输出包含全局上下文信息,Infini-attention将Memory Retrieve的结果\(A_{mem}\)与Local Attention的输出\(A_{dot}\)通过可学习的门控标量\(\beta\)进行融合: \[ A=\text{sigmoid}(\beta)\odot A_{mem}+(1-\text{sigmoid}(\beta))\odot A_{dot}. \] 门控机制的引入可以使模型能更好权衡长期记忆和局部信息。对于多头的Infini-attention,可以并行计算\(H\)个头的注意力输出并将其拼接在一起,通过一个可训练的投影矩阵\(W^O \in \mathbb{R}^{H \times d_{value} \times d_{model}}\)得到最终的输出\(O \in \mathbb{R}^{N \times d_{model}}\): \[ O=\text{concat}(A^1,\cdots,A^H)W^O. \]
2.3.3 Memory Update
retrieve完成之后,就可以用当前片段的\(KV\)信息更新压缩记忆和归一化因子: \[ M_s\leftarrow M_{s-1}+\sigma(K)^TV\mathrm{~and~}z_s\leftarrow z_{s-1}+\sum_{t=1}^N\sigma(K_t). \] 新的记忆状态\(M_s\)和归一化因子\(z_s\)将用于下一片段的Retrieve,这样就实现了全局上下文信息的传递。
上述\(M_s\)的更新方式称之为Linear Update,受delta rule的启发,作者还提出了一种以增量规则为基础的更新方式,称之为Linear+Delta: \[ M_s\leftarrow M_{s-1}+\sigma(K)^T(V-\frac{\sigma(K)M_{s-1}}{\sigma(K)z_{s-1}}). \] 与Linear Update相比,Delta方式会先从\(V\)中减去\(\frac{\sigma(K)M_{s-1}}{\sigma(K)z_{s-1}}\),被减去的这项可以看成是用\(K\)去检索\(M_{s-1}\)并得到压缩记忆中的存储的\(V_{mem}\),那么更新记忆时已有的\(V_{mem}\)就会被减去,通过增量更新的方式可以减少记忆中的冗余信息。
3. Linear Auto-regressive Attention
Infini-attention中Compressive Memory本质上是一种Linear Auto-regressive Attention,文中使用了一些kenel trick的方法来代替全局\(\text{softmax}\)的计算,但这并不是一个新概念,围绕的Linear attention的研究已经有很多。下面来论证为什么Infini-attention是Linear Auto-regressive Attention的变体。
对于Scaled-Dot Attention,其形式为: \[ Attention(Q,K,V)=\text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V. \] \(QK^{\top}\)得到一个\(N \times N\)的矩阵,这一步决定了Attention的复杂度为\(O(N^2)\),如果没有\(\text{softmax}\)一步,那么可以先计算\(K^TV\)得到一个\(d \times d\)的矩阵,然后再用\(Q\)左乘它,这样的计算复杂度为\(O(Nd^2)\),由于\(d \ll N\),因此Linear Attention的复杂度大致为\(O(N)\)。所以Linear Attention主要探究的是如何摘掉\(\text{softmax}\)这一步。
我们先将Scaled-Dot Attention等价改写为: \[ Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})_i = \frac{\sum\limits_{j=1}^n e^{\boldsymbol{q}_i^{\top}\boldsymbol{k}_j}\boldsymbol{v}_j}{\sum\limits_{j=1}^n e^{\boldsymbol{q}_i^{\top}\boldsymbol{k}_j}} \] 所以Scaled-Dot Attention是以\(e^{\boldsymbol{q}_{i}^{\top}\boldsymbol{k}_{j}}\)为权重对\(\boldsymbol{v}_i\)进行加权平均,而正是由于这个指数项,使得无法先计算\(k_j\)和\(v_j\)。目前有一种使用kernel trick的方法,可以将\(e^{\boldsymbol{q}_{i}^{\top}\boldsymbol{k}_{j}}\)的计算用\(\phi(\boldsymbol{q}_i)^\top\varphi(\boldsymbol{k}_j)\)替换,其中\(\phi(\cdot)\)和\(\varphi(\cdot)\)是值域非负的激活函数。对于自回归生成模型需要Mask未来信息,因此将求和\(\sum\limits_{j=1}^n\)改为\(\sum\limits_{j=1}^i\),Attention的计算可以改写为: \[ Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})_i = \frac{\sum\limits_{j=1}^i \left(\phi(\boldsymbol{q}_i)^{\top} \varphi(\boldsymbol{k}_j)\right)\boldsymbol{v}_j}{\sum\limits_{j=1}^i \phi(\boldsymbol{q}_i)^{\top} \varphi(\boldsymbol{k}_j)}=\frac{ \phi(\boldsymbol{q}_i)^{\top} \sum\limits_{j=1}^i\varphi(\boldsymbol{k}_j)\boldsymbol{v}_j^{\top}}{ \phi(\boldsymbol{q}_i)^{\top} \sum\limits_{j=1}^i\varphi(\boldsymbol{k}_j)} \] 上述Attention可以作为一个RNN模型以递归的方式实现,设\(\boldsymbol{S}_i=\sum\limits_{j=1}^i\varphi(\boldsymbol{k}_j)\boldsymbol{v}_j^{\top}\),\(\boldsymbol{z}_i=\sum\limits_{j=1}^i\varphi(\boldsymbol{k}_j)\),则有: \[ Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})_i =\frac{ \phi(\boldsymbol{q}_i)^{\top} \boldsymbol{S}_i}{ \phi(\boldsymbol{q}_i)^{\top} \boldsymbol{z}_i},\quad \begin{aligned}&\boldsymbol{S}_i=\boldsymbol{S}_{i-1}+\varphi(\boldsymbol{k}_i)\boldsymbol{v}_i^{\top}\\ &\boldsymbol{z}_i=\boldsymbol{z}_{i-1}+\varphi(\boldsymbol{k}_i) \end{aligned} \] 到此可以看出Inifi-attention的Compressive Memory模块就是一个Linear Auto-regressive Attention,只不过Inifi-attention中Memory的Retrieve和Update是以Segment为单位进行的,而Linear Auto-regressive Attention是以Token为单位进行的;另一点就是Inifi-attention是先Retrieve再Update,与Linear Auto-regressive Attention相反。
4. Is this a gold solution?
抛开创新性,Infini-attention使用RNN的架构来记忆全局上下文信息,理论上可以处理无限长的文本,但是这种记忆是不可学习的,模型无法知道哪些高质量信息需要保留在压缩记忆中。jlamprou提出了一些可学习的压缩记忆方案,例如Differentiable Neural Computer (DNC),将可训练的神经网络控制器和可读写的外部存储器进行结合从而控制信息的流动。另一点就是模型无法并行训练,每一个片段的计算都依赖于上一个片段的计算,这样会导致训练效率低下。
总之,Infini-Transformer是一个很有趣的模型,通过Local Attention + RNN能够处理无限长的文本,但是由于RNN固有的缺点,Infini-Transformer并没有很好地解决Background提出的记忆压缩问题,因此在记忆压缩中引入可控或可学习的机制将会是有趣的研究方向。

微信支付

支付宝支付