如何理解RNN中的梯度消失
本文最后更新于 2024年4月11日 下午
本文阐明了RNN中的梯度消失问题的含义,并根据反向传播公式深入分析了RNN中梯度消失的原因,最后说明了梯度消失和长距离依赖之间的关系。
1. DNN中的梯度消失
在分析RNN梯度消失的原因之前,我们先回顾一下DNN(多层感知机)中梯度消失是如何产生的。
考虑一个具有n个隐藏层的DNN,前向传播时第\(i\)个隐层的输出作为第\(i+1\)个隐层的输入: \[ \begin{array}{l} \mathbf{H}^{(1)}&=\sigma\left(\mathbf{W}^{(1)} \mathbf{X} +\mathbf{b}^{(1)}\right) \\ \dots\\ \mathbf{H}^{(n)}&=\sigma\left(\mathbf{W}^{(n)} \mathbf{H}^{(n-1)} +\mathbf{b}^{(n)}\right) \\ \mathbf{O}&= \mathbf{W}^{(n+1)} \mathbf{H}^{(n)}+\mathbf{b}^{(n+1)}. \end{array} \tag{1} \] 损失函数为: \[ L = l(\mathbf{O},\mathbf{Y}) \tag{2} \] 反向传播时根据链式法则有: \[ \begin{aligned} \frac{\partial L}{\partial \mathbf{W}^{(i)}} &= \frac{\partial l}{\partial \mathbf{O}} \frac{\partial \mathbf{O}}{\partial \mathbf{H}^{(n)}} \frac{\partial \mathbf{H}^{(n)}}{\partial \mathbf{H}^{(n-1)}} \dots \frac{\partial \mathbf{H}^{(i)}}{\partial \mathbf{W}^{(i)}} \\ & = \frac{\partial l}{\partial \mathbf{O}} \frac{\partial \mathbf{O}}{\partial \mathbf{H}^{(n)}} \left(\prod_{j=i}^{n-1} \frac{\partial \mathbf{H}^{(j+1)}}{\partial \mathbf{H}^{(j)}}\right) \frac{\partial \mathbf{H}^{(i)}}{\partial \mathbf{W}^{(i)}} \\ \end{aligned} \tag{3} \]
\(\frac{\partial l}{\partial \mathbf{O}}\)、\(\frac{\partial \mathbf{O}}{\partial \mathbf{H}^{(n)}}\)和\(\frac{\partial \mathbf{H}^{(i)}}{\partial \mathbf{W}^{(i)}}\)都很容易计算,我们重点关注\(\prod_{j=i}^{n-1}\frac{\partial \mathbf{H}^{(j+1)}}{\partial \mathbf{H}^{(j)}}\)这一部分,对于连乘中的任意一项有: \[ \frac{\partial \mathbf{H}^{(j+1)}}{\partial \mathbf{H}^{(j)}} = {\mathbf{W}^{(j)}}^\top \odot {\sigma}'(\mathbf{W}^{(j)} \mathbf{H}^{(j-1)} +\mathbf{b}^{(j)}) \tag{4} \] 其中\({\sigma}'(\mathbf{W}^{(j)} \mathbf{H}^{(j-1)} +\mathbf{b}^{(j)})\)是激活函数的导数,若选用\(\tanh\)作为激活函数,则\({\sigma}' \in (0,1]\);若选用\(\mathrm{sigmoid}\)作为激活函数,则\({\sigma}' \in (0,0.25]\),可见二者的导数值都不大于1。
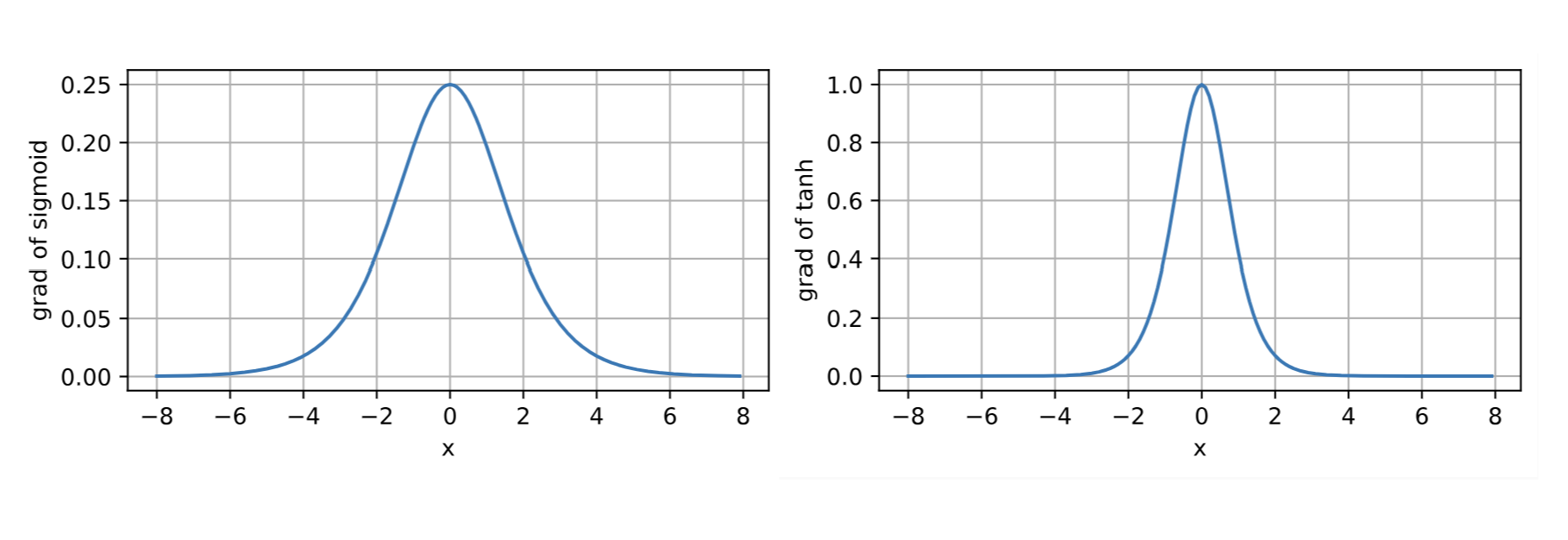
对于\(\prod_{k=i}^{n-1}\frac{\partial \mathbf{H}^{(k+1)}}{\partial \mathbf{H}^{(k)}} = \prod_{k=i}^{n-1} {\mathbf{W}^{(k)}}^\top \odot{\sigma}'(\mathbf{W}^{(k)}\mathbf{H}^{(k-1)} +\mathbf{b}^{(k)})\),当\(i\)较小时,也就是反向传播到靠近输入层时,将会出现多个参数矩阵\({\mathbf{W}^{(j)}}^\top\)和多个\({\sigma}'\)连乘,多个矩阵连乘可能会导致梯度以指数速度增大或减小,而多\({\sigma}'\)个连乘则会导致梯度以指数速度减小,因为\({\sigma}'\)恒小于1。当二者综合表现为减小的趋势时,就有可能发生梯度消失。
总结一下就是在反向传播的过程中,用于训练参数的目标函数值,也就是loss,会随着距离的增加会呈指数级减小,因此在对靠近输入层的参数求偏导得到的梯度值也会呈指数级减小。这个问题的直接后果就是靠近输入层的一些层的参数很少会更新,或者说更新幅度很小。
2. RNN中的梯度消失
现在我们以同样的方式来推导RNN中的反向传播公式。不过需要注意的是,在DNN中每一个隐层有单独的一个参数矩阵,每层的参数矩阵不共享,在RNN中,我们将RNN中每一个时间步视为一层,每一层的参数是共享的,因此我们可以将RNN展开看成共享参数的多层感知机。
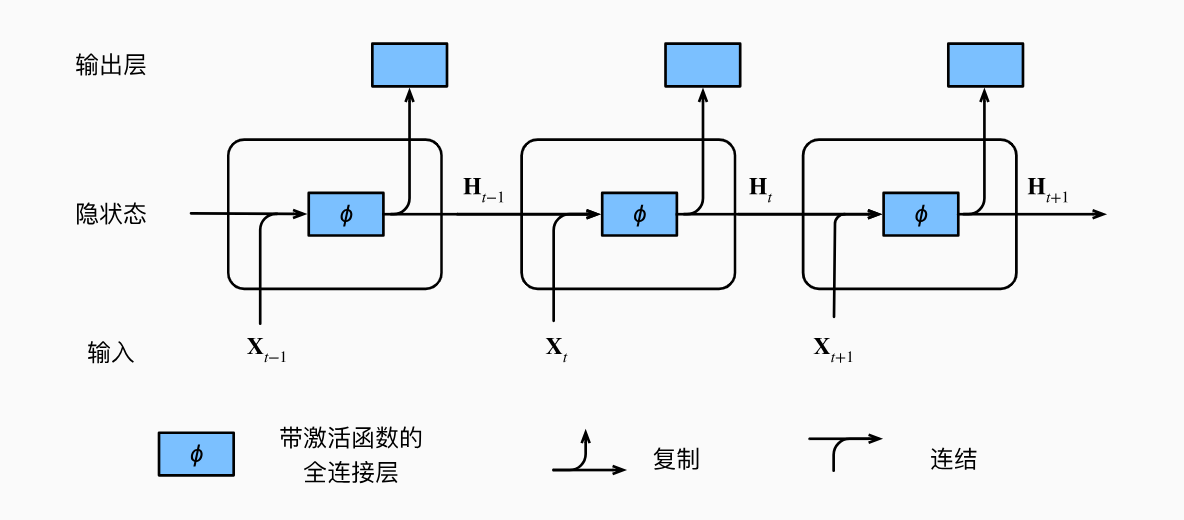
为了保持简单,我们考虑一个没有偏置参数的循环神经网络,有以下前向传播公式: \[ \begin{aligned} \mathbf{h}_t &= \sigma \left( \mathbf{W}_{hx} \mathbf{x}_t + \mathbf{W}_{hh} \mathbf{h}_{t-1} \right) ,\\ \mathbf{o}_t &= \mathbf{W}_{qh} \mathbf{h}_{t},\\ \end{aligned} \tag{5} \] 与DNN只在最后输出层才会输出值用于误差计算不同,RNN在每一个时间步都会有输出,并且输出的值最终都会参与误差计算。用\(l_t(\mathbf{o}_t, y_t)\)表示时间步\(t\)处的损失函数,反向传播时,需要分别计算\(\frac{\partial l_t}{\partial \mathbf {W}_{hx}}\)、\(\frac{\partial l_t}{\partial \mathbf {W}_{hh}}\)、\(\frac{\partial l_t}{\partial \mathbf {W}_{qh}}\)
其中\(\frac{\partial l_t}{\partial \mathbf {W}_{qh}}\)很好计算: \[ \frac{\partial l_t}{\partial \mathbf{W}_{qh}} = \frac{\partial l_t}{\partial \mathbf{o}_t} \frac{\partial \mathbf{o}_t}{\partial \mathbf{W}_{qh}} = \frac{\partial l_t}{\partial \mathbf{o}_t} \mathbf{h}_t^\top \tag{6} \] 但是\(\frac{\partial l_t}{\partial \mathbf W_{hx}}\)、\(\frac{\partial l_t}{\partial \mathbf W_{hh}}\)的计算要复杂的多,目标函数\(l_t\)通过\(\mathbf{o}_{t}\),\(\mathbf{o}_{t}\)通过\(\mathbf{h}_{t}\)直接或通过隐状态\(\mathbf{h}_1, \ldots, \mathbf{h}_{t-1}\)间接依赖于隐藏层中的模型参数\(\mathbf{W}_{hx}\)和\(\mathbf{W}_{hh}\),也就是说隐状态\(\mathbf{h}_1, \ldots, \mathbf{h}_{t}\)均参与了\(l_t\)对\(\mathbf{W}_{hx}\)和\(\mathbf{W}_{hh}\)梯度的计算,整体的梯度是时间步从0-t的梯度之和。
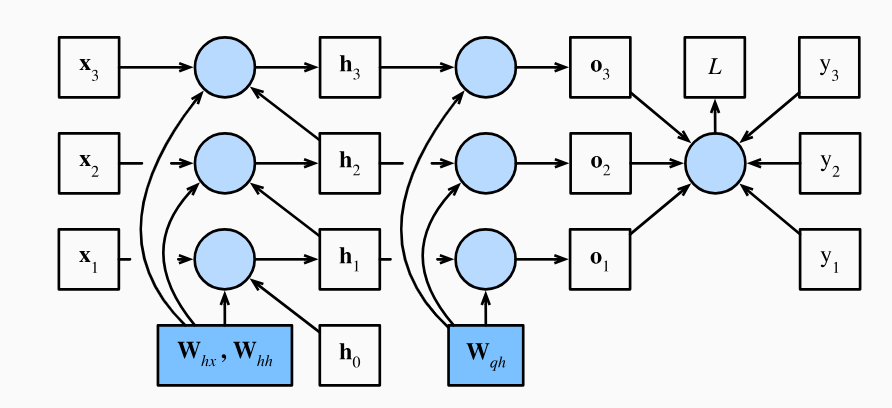
根据链式法则可以得到: \[ \begin{aligned} \frac{\partial l_t}{\partial \mathbf{W}_{hx}} &= \sum_{i=1}^t \frac{\partial l_t}{\partial \mathbf{o}_t} \frac{\partial \mathbf{o}_t}{\partial \mathbf{h}_{t}} \frac{\partial \mathbf{h}_t}{\partial \mathbf{h}_{i}}\frac{\partial \mathbf{h}_i}{\partial \mathbf{W}_{hx}} ,\\ \frac{\partial l_t}{\partial \mathbf{W}_{hh}} &= \sum_{i=1}^t \frac{\partial l_t}{\partial \mathbf{o}_t} \frac{\partial \mathbf{o}_t}{\partial \mathbf{h}_{t}} \frac{\partial \mathbf{h}_t}{\partial \mathbf{h}_{i}}\frac{\partial \mathbf{h}_i}{\partial \mathbf{W}_{hh}} \end{aligned} \tag{7} \] 其中\(\frac{\partial \mathbf{h}_t}{\partial \mathbf{h}_{i}}\)计算需要再次用到链式法则: \[ \frac{\partial \mathbf{h}_t}{\partial \mathbf{h}_{i}} = \frac{\partial \mathbf{h}_t}{\partial \mathbf{h}_{t-1}} \frac{\partial \mathbf{h}_{t-1}}{\partial \mathbf{h}_{t-2}} \dots \frac{\partial \mathbf{h}_{i+1}}{\partial \mathbf{h}_{i}} = \prod_{k=i}^{t-1} \frac{\partial \mathbf{h}_{k+1}} {\partial \mathbf{h}_{k}} \tag{8} \] 对于连乘中任意一项有: \[ \frac{\partial \mathbf{h}_{k+1}}{\partial \mathbf{h}_{k}} = \mathbf{W}_{hh}^{\top} \odot \sigma' \left( \mathbf{W}_{hx} \mathbf{x}_k + \mathbf{W}_{hh} \mathbf{h}_{k-1} \right) \tag{9} \] 记\(\sigma_{k}' =\sigma' \left( \mathbf{W}_{hx} \mathbf{x}_k + \mathbf{W}_{hh} \mathbf{h}_{k-1} \right)\),则有: \[ \frac{\partial \mathbf{h}_t}{\partial \mathbf{h}_{i}} = \prod_{k=i}^{t-1} \frac{\partial \mathbf{h}_{k+1}} {\partial \mathbf{h}_{k}} = \prod_{k=i}^{t-1} \mathbf{W}_{hh}^{\top} \odot \sigma_{k}' \tag{10} \] 我们发现式\((10)\)和DNN中式\((4)\)出现了同样的问题:当\(i\)很小时,矩阵高次幂带来的不稳定性和激活函数的导数连乘带来的指数速度的衰减有可能导致偏导数\(\frac{\partial \mathbf{h}_t}{\partial \mathbf{h}_{i}}\)的爆炸或消失。但是要由\(\frac{\partial\mathbf{h}_t}{\partial \mathbf{h}_{i}}\)消失推出梯度消失还存在一个问题:\(\frac{\partial \mathbf{h}_t}{\partial \mathbf{h}_{i}}\)很小只能代表\(\frac{\partial l_t}{\partial \mathbf{W}_{hx}}\)计算式\((7)\)中某一项很小,\(\frac{\partial l_t}{\partial \mathbf{W}_{hx}}\)整体由于是各个项的累加,因此基本不会因为某一项的消失而导致总体的消失,那么何来梯度消失这一说法呢?实际上RNN中确实会发生梯度消失,但是梯度消失在RNN相对于DNN有着不同的含义。
我们不妨再回顾DNN和RNN模型之间的区别:
在DNN中,每层有单独的参数,反向传播时,目标函数到任意一层参数有且仅有1条路径,因此在式\((3)\)中没有出现多条路径梯度的累加,如果唯一的1条路径上发生梯度消失就会使整体的梯度消失。
在RNN中,每一个时间步共享参数矩阵\(\mathbf{W}_{hx}\)和\(\mathbf{W}_{hh}\),目标函数到参数\(\mathbf{W}_{hx}\)和\(\mathbf{W}_{hh}\)有多条路径。举个例子,求\(l_3\)对\(\mathbf{W}_{hx}\)的梯度,由图可以看出一共有3条路径,分别用红、绿、蓝标出。反向传播时,对于参数从源节点到目标函数的每条路径,我们都需要计算沿着该路径的梯度,并将这些梯度相加以得到该目标函数对该参数的总梯度。
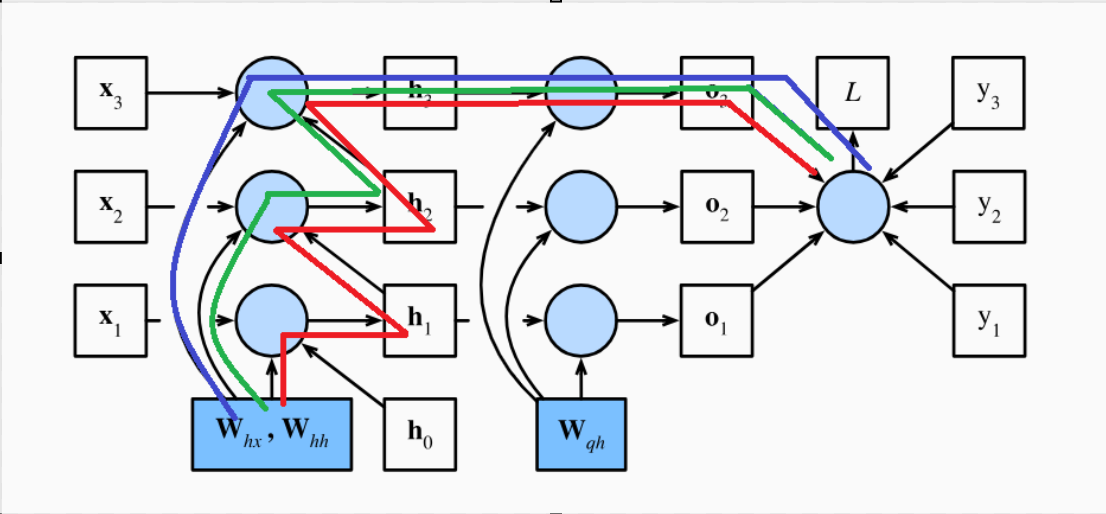
对于\(\frac{\partial l_t}{\partial \mathbf{W}_{hx}} = \sum_{i=1}^t \frac{\partial l_t}{\partial \mathbf{o}_t} \frac{\partial \mathbf{o}_t}{\partial \mathbf{h}_{t}} \frac{\partial \mathbf{h}_t}{\partial \mathbf{h}_{i}}\frac{\partial \mathbf{h}_i}{\partial \mathbf{W}_{hx}}\)中的任意一项梯度\(\frac{\partial l_t}{\partial \mathbf{o}_t} \frac{\partial \mathbf{o}_t}{\partial \mathbf{h}_{t}} \frac{\partial \mathbf{h}_t}{\partial \mathbf{h}_{i}}\frac{\partial \mathbf{h}_i}{\partial \mathbf{W}_{hx}}\),其实就代表\(l_t\)到\(\mathbf{W}_{hx}\)的一条路径,只不过这些路径有长有短。路径越长,对应的\(\frac{\partial \mathbf{h}_t}{\partial \mathbf{h}_{i}}\)产生的乘法链就越长,由式\((10)\)可以看出该路径的梯度就会越可能消失,但是只要其他路径上还存在梯度就不会导致整体梯度的消失。因此RNN 中总的梯度是不会消失的,即便梯度越传越弱,那也只是远距离的梯度消失,由于近距离的梯度不会消失,所有梯度之和便不会消失。
那么RNN中远距离的梯度消失与RNN捕捉不到长距离依赖有什么关系呢?
我们仍从表达式来分析,将梯度\(\frac{\partial l_t}{\partial \mathbf{o}_t} \frac{\partial \mathbf{o}_t}{\partial \mathbf{h}_{t}} \frac{\partial \mathbf{h}_t}{\partial \mathbf{h}_{i}}\frac{\partial \mathbf{h}_i}{\partial \mathbf{W}_{hx}}\)合并一部分写成\(\frac{\partial l_t}{\partial \mathbf{h}_i} \frac{\partial \mathbf{h}_i}{\partial \mathbf{W}_{hx}}\),从数学角度来看,\(\frac{\partial l_t}{\partial \mathbf{h}_i}\)描述的是损失函数\(l_t\)对隐状态 \(\mathbf{h}_i\)的偏导数,它反映了 \(\mathbf{h}_i\) 的微小变化如何影响 \(l_t\)。在RNN中,长期依赖可以被理解为当前的输出(或者损失函数)对过去较早时间步的隐状态的依赖,这种依赖可以通过 \(\frac{\partial l_t}{\partial \mathbf{h}_i}\) 来捕捉。
对于梯度 \(\frac{\partial l_t}{\partial \mathbf{h}_i} \frac{\partial \mathbf{h}_i}{\partial \mathbf{W}_{hx}}\),损失函数\(l_t\)对隐状态 \(\mathbf{h}_i\)的依赖信息作为梯度构成的一部分,通过作用于梯度来影响参数的更新。如果依赖信息 \(\frac{\partial l_t}{\partial \mathbf{h}_i}\) 很小,会导致梯度\(\frac{\partial l_t}{\partial \mathbf{h}_i} \frac{\partial \mathbf{h}_i}{\partial \mathbf{W}_{hx}}\)也很小(梯度消失),那么这些依赖信息对参数更新的影响也会很小,网络可能无法有效地学习到这些长距离的依赖信息,也就是捕捉不到长距离依赖。
所以RNN中梯度消失的真正含义是:在梯度更新时,由于长距离的依赖关系较弱,近距离依赖关系对整体梯度构成的影响更大,梯度被近距离的梯度主导,模型更倾向于利用近距离的梯度来更新参数,导致难以学到长距离的依赖关系。
最后举一个语言建模的例子来充分理解长期依赖的含义:
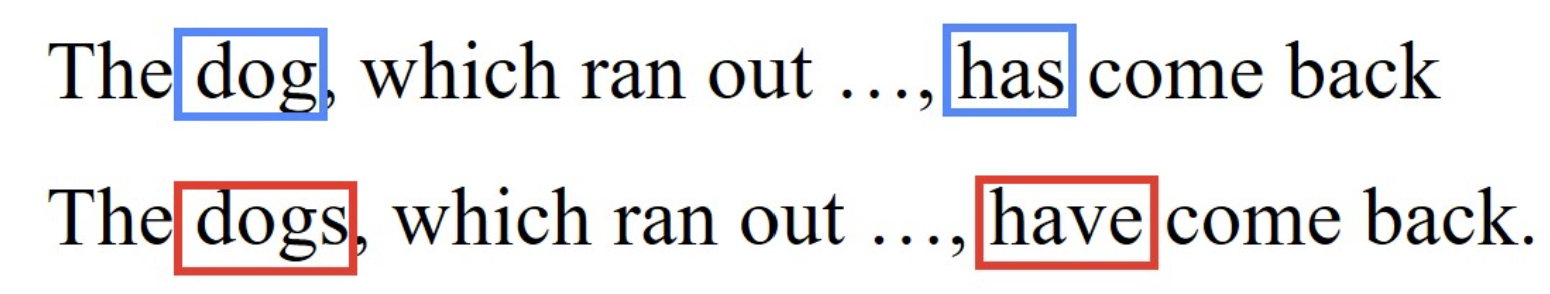
观察上述两个例子,会发现句子开头的“Dog”这个词影响了位于最后的单词“has”,如果我们将单数词改为复数词“Dogs”,则应该将单词“has”改为"have"。对于上述例句,中间的句子可能会很长,位于末尾的单词受到几乎位于该句子开头的单词的影响,这就是我们所说的“长期依赖” 。
要想捕捉这种长期依赖,可以选择更复杂的LSTM和GRU模型,关于LSTM和GRU是如何缓解梯度消失的,推荐参考【也来谈谈RNN的梯度消失/爆炸问题】中的论证。
【参考】

微信支付

支付宝支付