详细解读AUC及其在推荐系统中的应用

在面试算法岗时，面试官经常会问关于AUC的一些问题，比如AUC的定义，AUC的计算方法，AUC的优缺点等等。本文将深入浅出地介绍AUC的含义、计算方法及其在推荐系统中的应用。

应用情景

在介绍AUC之前我们先来考虑一个实际的推荐情景：假设现在商品库里有6件物品，分别是\(\{A, B, C, D, E, F\}\)，而你实际感兴趣的只有\(\{B,D,F\}\)这两件物品，假设推荐系统预测你对这6件物品的兴趣的顺序为\(\{A, B, C, D, E, F\}\)，如果推荐系统只能推荐3件物品，那么被推荐的物品为\(\{A, B, C\}\)，也就是说你感兴趣3件物品中只有1件物品被推荐出来了，而3件不感兴趣的物品中有2件物品被推荐出来了，很明显\(\frac{1}{3} < \frac{2}{3}\)，说明推荐系统的推荐效果不好。

如何衡量推荐效果

我们将用户感兴趣的商品称为正例，不感兴趣的商品称为负例。经过分类器决策后，数据可以被划分成4个部分：TP(True Positive)、FP(False Positive)、TN(True Negative)、FN(False Negative)，positive和negative表示预测的类别，而true和false表示预测的正确性，在我们的情境中，\(TP\)为\(\{B\}\)，\(FP\)为\(\{A,C\}\)，\(TN\)为\(\{E\}\)，\(FN\)为\(\{D,F\}\)。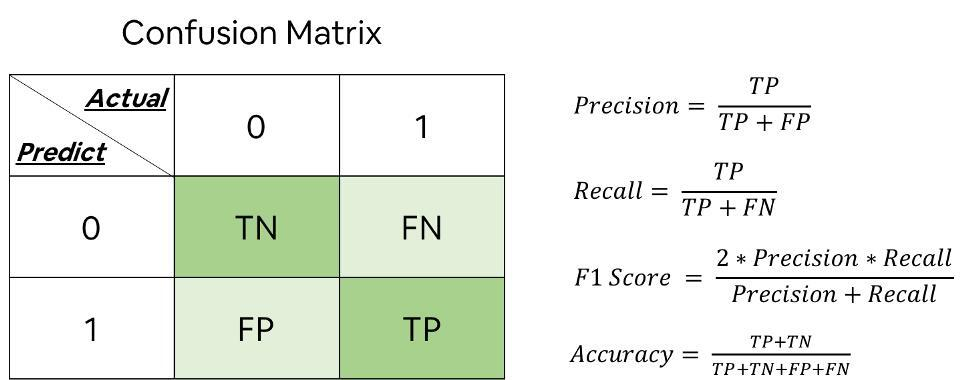

有了上述定义，我们就可以引入两个概念：TPR(True Positive Rate)、FPR(False Positive Rate) \[ \begin{split}\begin{aligned} TPR &= \frac{TP}{TP + FN} \\ FPR &= \frac{FP}{FP + TN} \end{aligned}\end{split} \] 在推荐系统中，\(TPR\)表示用户感兴趣的物品被推荐出来的概率（上文提到的\(\frac{1}{3}\)，也称为recall），\(FPR\)表示用户不感兴趣的物品被推荐出来的概率（上文提到的\(\frac{2}{3}\)）。比较\(TPR\)和\(FPR\)的大小可以得出以下结论： - 当\(TPR > FPR\)时，说明推荐系统的推荐效果不错，推荐的物品中用户感兴趣的物品占总感兴趣物品的比例较大 - 当\(TPR < FPR\)时，说明推荐系统的推荐效果不好，推荐的物品中用户感兴趣的物品占总感兴趣物品的比例较小 - 当\(TPR = FPR\)时，说明推荐系统对任意一个物品推荐和不推荐的概率相等。

ROC和AUC的定义

在上述的情景中，我们知道如果推荐系统推荐的商品总数是确定的，那么TPR和FPR是确定的，我们可以通过改变推荐的商品总数来获取多组TPR和FPR。例如我们将推荐的商品总数改为4，那么被推荐的物品为\(\{A, B, C,D\}\)，TPR和FPR计算如下： \[ \begin{split}\begin{aligned} TPR &= \frac{TP}{TP + FN} = \frac{2}{2+1} \\ FPR &= \frac{FP}{FP + TN} = \frac{2}{2+1} \end{aligned}\end{split} \]

我们将多组TPR和FPR在二维坐标系中绘制出来，横坐标为FPR，纵坐标为TPR，并将这些点连接起来就得到了ROC（Receiver Operating Characteristic）曲线（下图与情景无关）：

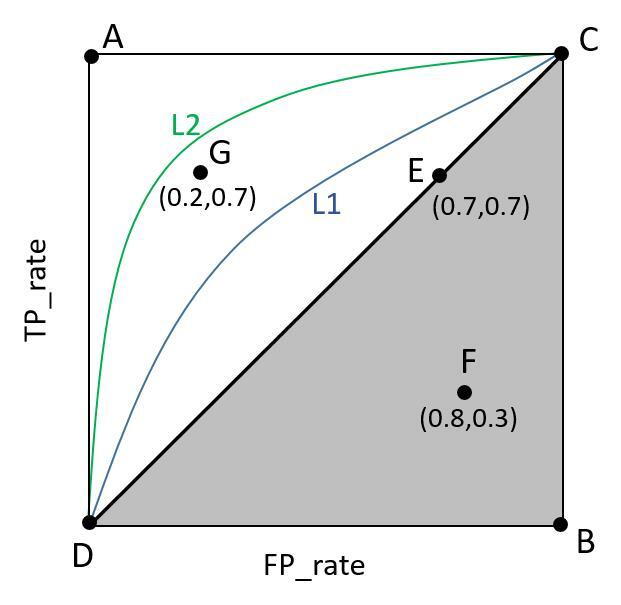
图中，A，G点表示模型有一定的甄别能力（TPR>FPR），其中A点对应一个完美分类器，所有正例都能被正确分类（TPR=1），所有负例没有被识别错误（FPR=0）。F点就是分类器太差了（TPR < FPR）。E点表示随机分类（TPR=FPR），即以50%的概率随机猜测。

而AUC（Area Under Curve）就是ROC曲线下的面积，AUC的取值不大于1，AUC越大，说明模型的性能越好，AUC=1表示模型的性能最好。

sklearn.metrics.roc_auc_score函数可以计算AUC值，这里简单介绍一下其实现过程。 roc_auc_score函数接收scores和labels两个参数，其中scores表示模型预测的评分，分数越高表示用户对该物品的兴趣可能越大，labels表示真实的标签，1表示用户感兴趣，0表示用户不感兴趣。

为了获取多组TPR和FPR，会先对scores进行排序，然后遍历scores，每次将一个score作为阈值（也就是上文提到的改变推荐的商品总数），将scores中大于等于该阈值的样本预测为正例，小于该阈值的样本标预测负例，这样就可以得到TP、FP、TN、FN。

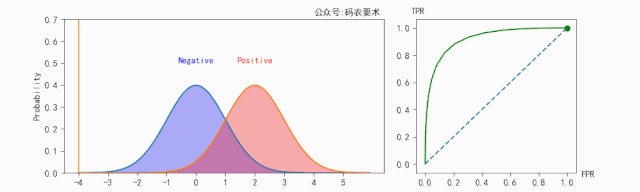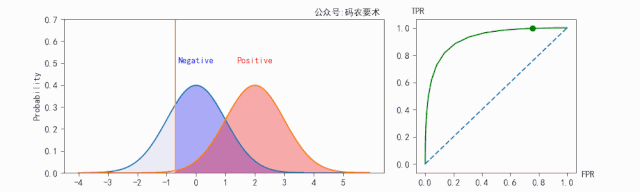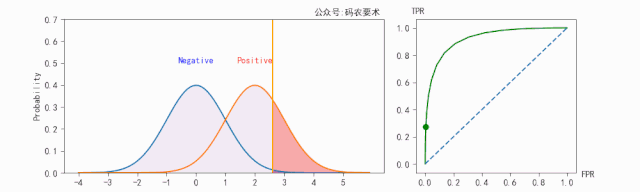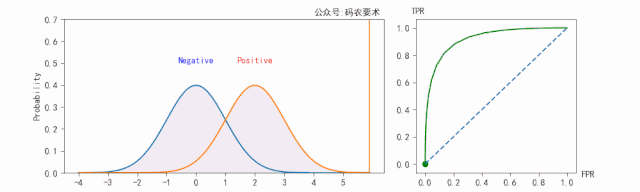
TPR的计算如下图所示：

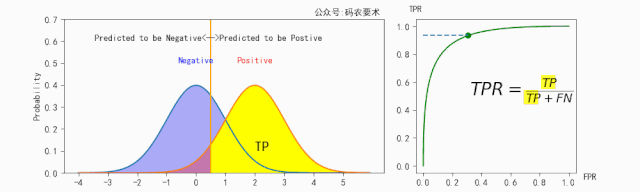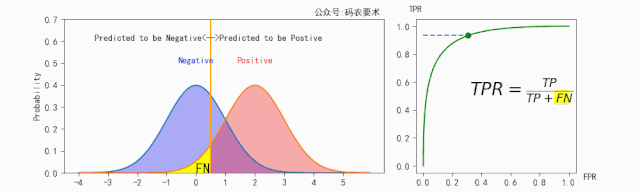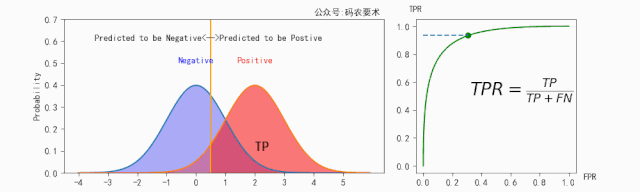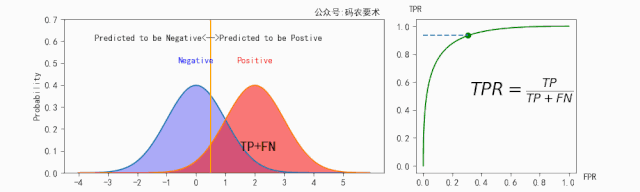
FPR的计算如下图所示：

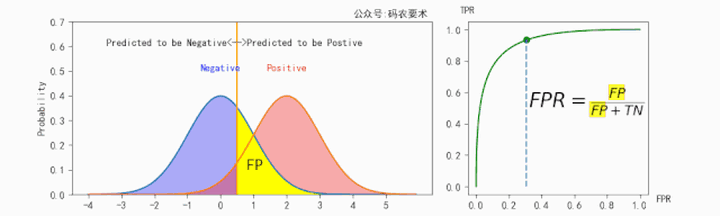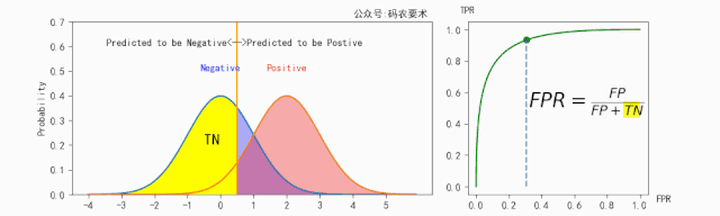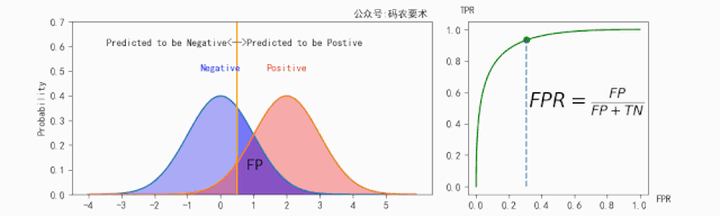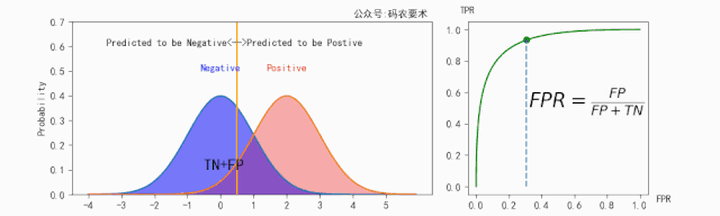
不同的阈值会得到不同的TPR和FPR，遍历阈值将多组TPR和FPR绘制成ROC曲线，如下图：

然后计算ROC曲线下小梯形面积之和即为AUC值。

AUC的含义

上述内容我们介绍了AUC的计算方法，那么AUC这个面积具体有什么含义呢？我们将ROC曲线视为\(TPR\)关于\(FPR\)的函数，即\(TPR = F(x)\)，那么AUC就是对这个函数进行积分，如下所示：

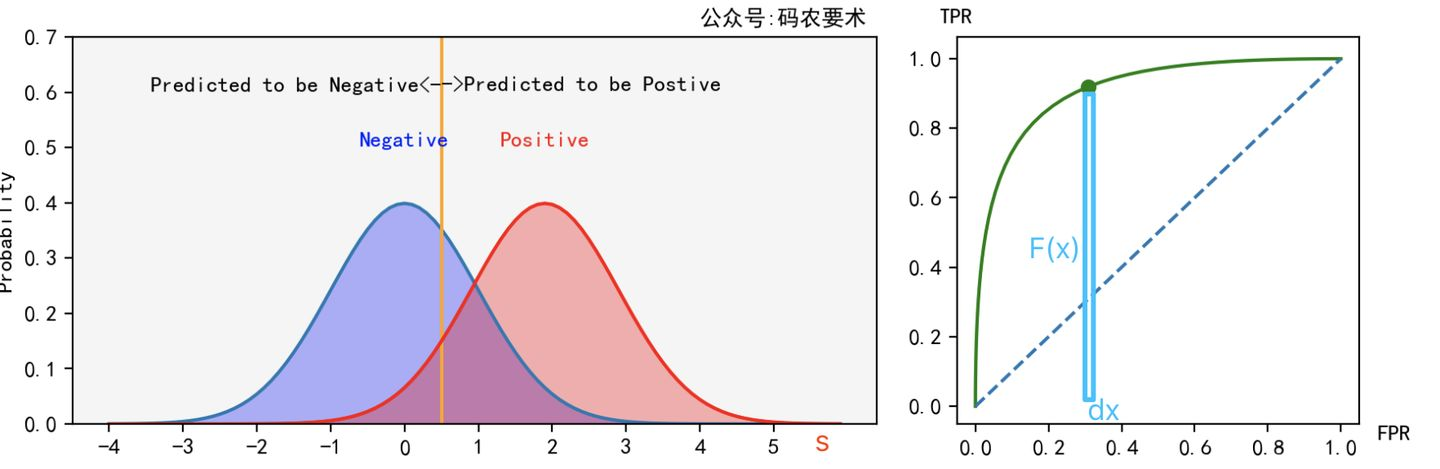
\[ AUC = \int_{0}^{1} F(x)dx \] 假设样本标签为\(y\)，模型预测得分为\(s\)，阈值为\(t\)，模型预测正例的概率密度函数为\(f_1(s)\)，预测负例的概率密度函数为\(f_0(s)\)，由于\(x\)是\(s\)和\(t\)的函数，因此我们可以将\(F(x)\)和\(x\)均看作是\(s\)和\(t\)的函数，则有： \[ \begin{split}\begin{aligned} TPR &= F(x) = \int_{t}^{\infty} f_1(s)ds = P(s>t|y=1) \\ FPR &= x = \int_{t}^{\infty} f_0(s)ds \end{aligned}\end{split} \]

\(x\)是\(t\)的变下限积分函数，\(x\)对\(t\)求导可得： \[ \begin{split}\begin{aligned} \frac{dx}{dt} &= -f_0(t) \\ dx &= -f_0(t)dt = -P(s^{\prime}=t|y^{\prime}=0)dt \end{aligned}\end{split} \] 这里\(s^{\prime}\)和\(y^{\prime}\)只是为了与正例的\(s\)和\(y\)区分开来，\(P(s^{\prime}=t|y^{\prime}=0)\)表示在样本标签为0的情况下，模型预测得分为\(t\)的概率。则有： \[ \begin{aligned} AUC& =\int_0^1F(x)dx \\ &=\int_\infty^{-\infty}F(x)(-f_0(t))dt \\ &=\int_{-\infty}^\infty F(x)f_0(t)dt \\ &=\int_{-\infty}^\infty P(s>t|y=1)f_0(t)dt \\ &=\int_{-\infty}^\infty P(s>t|y=1)\times P(s^{\prime}=t|y'=0)dt \\ &=\int_{-\infty}^\infty P(s>t\land s^{\prime}=t|y=1\land y^{\prime}=0)dt \\ &=\int_{-\infty}^\infty P(s>s^{\prime}\land s^{\prime}=t|y=1\land y^{\prime}=0)dt \\ &=P(s>s^{\prime}|y=1\land y^{\prime}=1) \end{aligned} \] 这里对后面几步说明一下，\(P(s>t|y=1)\)表示对于正例样本，模型预测其得分大于阈值\(t\)的概率，\(P(s^{\prime}=t|y^{\prime}=0)\)表示对于负例样本，模型预测得分等于\(t\)的概率，这两个事件是相互独立的，因此二者的乘积就是\(P(s>t\land s^{\prime}=t|y=1\land y^{\prime}=0)\)，含义就是对于任意一个正例和负例，负例得分等于\(t\)，正例得分大于\(t\)的概率，对其在\(t\)上积分相当于遍历所有的阈值\(t\)，即对所有负例得分情况下正例得分大于负例得分的概率求和。

我们也可以从上述第四行推导\(AUC = \int_{-\infty}^\infty P(s>t|y=1)f_0(t)dt\)看出来，我们是对\(P(s>t|y=1)\)在所有\(t\)下加权求和，权重函数为\(f_0(t)\)，表示负例得分为\(t\)的概率，而\(P(s>t|y=1)\)表示正例得分大于\(t\)（也是负例得分）的概率。

最终结果\(P(s>s^{\prime}|y=1\land y^{\prime}=1)\)的含义是：对于任意一个正例和负例，模型评判正例得分大于负例得分的概率，这也是AUC的实际含义。

重写AUC

从上述结论我们可以知道，如果要评估推荐系统的AUC，只需从测试集中标签为正的样本集和标签为负的样本集生成所有的正例和负例对，然后计算模型判别正例得分大于负例得分的概率即可，不需计算TPR和FPR再绘图算面积了。

下面给出具体计算步骤： 将测试样本的模型评分从小到大排序，对于第\(i\)个正样本，其排名为\(r_i\)，那么这个正样本之前有\(r_i-1\)个样本，其中正样本个数为\(i-1\)个，负样本个数为\(r_i-1-(i-1)=r_i-i\)个，因此对于第\(i\)个正样本，有\(r_i-i\)个负样本得分小于正样本得分。设正样本个数为\(N_+\)，负样本个数为\(N_-\)，共有\(N_+N_-\)个正负样本对，其中有\(\sum_{i=1}^{N_+}(r_i-i)\)个正例得分大于负例得分，因此AUC的计算公式为： \[ AUC = \frac{\sum_{i=1}^{N_+}(r_i-i)}{N_+N_-} = \frac{\sum_{i=1}^{N_+}r_i - (N_+(N_+ + 1))/{2}}{N_+N_-} \] 为求出AUC需要求出以下3个值： 1. \(N_+\)：labels中正样本个数 2. \(N_-\)：labels中负样本个数 3. \(\sum_{i=1}^{N_+}r_i\)：所有正样本的排名之和

下面给出代码实现：

# scores为模型预测得分，labels为真实标签，1表示正样本，0表示负样本
def auc(scores,labels):
    pos_num = sum(labels)
    neg_num = len(labels) - pos_num
    ranked_socres = sorted([(score,label) for score,label in zip(scores,labels)],key=lambda x:x[0])
    pos_rank_sum = sum([rank+1 for rank,(score,label) in enumerate(ranked_socres,1) if label == 1]) # rank从1开始
    auc = (pos_rank_sum - pos_num*(pos_num+1)/2)/(pos_num*neg_num)
    return auc

实验测试

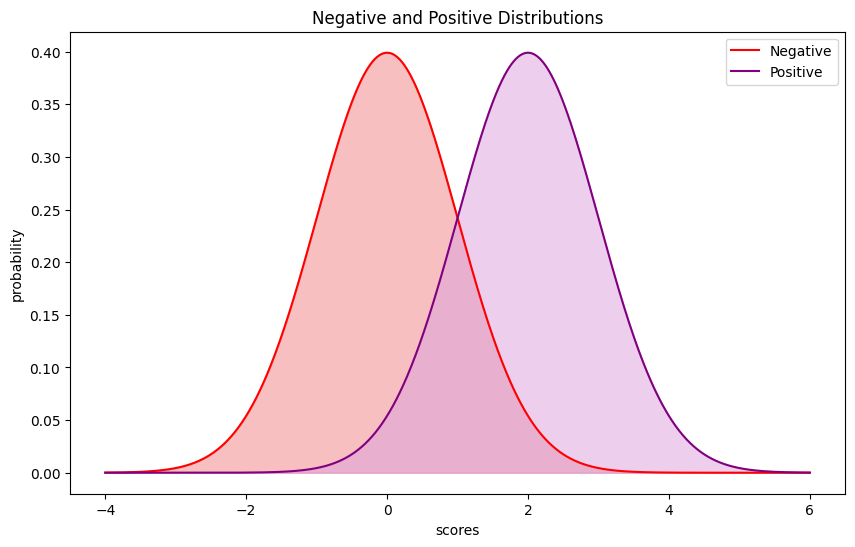
下面我们用一个例子来测试一下AUC函数，我们从正态分布\(N(0,1)\)中生成400个负样本，从\(N(2,1)\)中生成100个正样本，其分布如图所示：

测试代码如下：

labels =[]
scores = []
neg_samples = np.random.normal(0,1,400)
labels.extend([0]*400)
scores.extend(neg_samples)
pos_samples = np.random.normal(2,1,100)
labels.extend([1]*100)
scores.extend(pos_samples)
print('auc:',auc(scores,labels))
print('roc_auc_score:',roc_auc_score(labels,scores))

输出结果：

auc: 0.91515
roc_auc_score: 0.91265

可以看到AUC函数计算的结果与sklearn.metrics.roc_auc_score函数计算的结果非常接近。

AUC的性质

1. 对类别不平衡问题的鲁棒性

从公式可以看出，TPR的计算只局限于正例，而FPR的计算只局限于负例，如果模型能够很好地区分正例和负例的得分分布，那么数据的不平衡对AUC的影响不会很大，例如将上述实验正例采样数由100改为5，输出结果如下：

auc: 0.8985
roc_auc_score: 0.896

可以看出类别不平衡对AUC的影响并不大。而如果将正例的分布改为\(N(0.5,1)\)，输出结果如下：

auc: 0.613775
roc_auc_score: 0.6112749999999999

此时AUC的值有明显下降，因为此时模型评判正例和负例的得分分布重合度较高，不能对其进行很好的区分。

2. 适用于二分类问题

AUC只关注正例和负例的得分排序，而不关注具体的得分值，这也符合推荐系统的应用情景，即对于用户感兴趣的物品和不感兴趣的物品，我们总是希望能推荐感兴趣的物品，即正例的得分要大于负例的得分，至于高多少并不重要。

3. AUC高不代表其他指标优秀

AUC只关注预测的正负例的顺序关系，对于和label的拟合情况则不关注。比如正例得分都是0.2，负例得分都是0.1，AUC很完美，但是 loss就会比较大（理想情况下，正例的得分应该接近 1，负例的得分应该接近 0）。

此外在不均衡的样本上，AUC的表现可能很好，但precision可能比较差。比如\(TP=80，FN=20，FP=100，TN=6000\)，此时从ROC曲线上看效果很好，但是precision非常低。

【参考】

1. sklearn roc_auc_score源码解读 ↩︎