漫游推荐系统（四）—— 推荐系统的个性化排名

本文最后更新于 2024年8月18日晚上

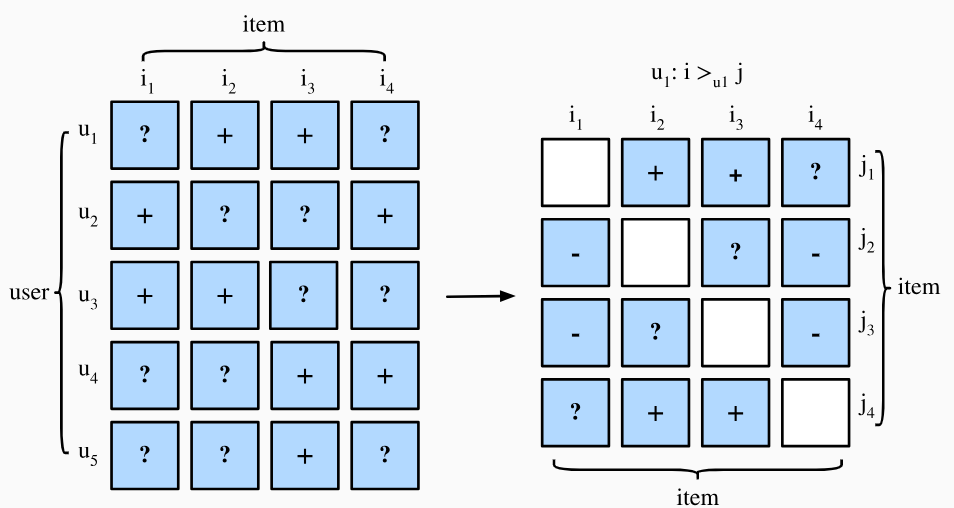
在之前关于矩阵分解模型和AutoRec模型中，我们只是对显示反馈进行了建模，即用户对物品的评分。但实际这种方式存在两种缺陷：真实场景下的反馈大多是隐式反馈，比如用户的点击、浏览等行为，并且收集显示反馈的成本较高。其次，只对显示反馈建模会忽略那些未观测到的用户-物品对（即用户没有明确给出评分或反馈的项目），其中可能包括负面反馈（用户对物品不感兴趣）和缺失值（用户未来可能会对物品产生反馈）。之前提到的两种模型选择简单地忽略这些缺失值，因此无法区分观测到和未观测到的用户-物品对，并且通常不适合个性化排名任务。

为此，能够对隐式反馈建模并生成排名推荐列表的推荐系统模型更受欢迎。一般来说，个性化排名系统可以通过逐点式（pointwise）、成对式（pairwise）和列表式（listwise）等方式进行优化：

逐点方法一次仅考虑单个用户-物品对，通过训练分类器（预测是否交互）或回归器（预测评分）来优化模型。矩阵分解模型和AutoRec模型都通过逐点目标进行优化。
成对方法考虑用户的一对项目，通过比较两个项目的分数来近似该对物品的最佳排序。这种方法通常会将用户的正样本（物品有交互）和负样本（与物品没有交互）进行比较，以便更好地区分用户的兴趣。通常成对方法更加适合排名任务，因为排名本质就是预测相对顺序。
列表方法则考虑用户的整个物品列表，通过优化排序模型来最大化整个列表的质量。列表方法要比成对方法更加复杂且计算更为密集，因为它需要考虑列表中的所有物品，而不仅仅是一对物品。

在本节我们将介绍两种成对方法的损失函数，贝叶斯个性化排序损失（Bayesian Personalized Ranking, BPR）和Hinge损失，以及他们各自的实现方式。

贝叶斯个性化排序损失

BPR损失是基于最大后验估计推导出来的，用于预测用户对不同物品的偏好顺序。BPR的训练数据包括一对正样本（用户与物品有交互）和一对负样本（用户与物品没有交互），并假设用户对正样本的偏好高于负样本。

我们使用\((u, i, j)\)元组定义训练数据，由用户\(u\)的一个正样本\(i\)和一个负样本\(j\)组成，含义为用户\(u\)对物品\(i\)的偏好高于物品\(j\)。在贝叶斯概率框架下，BPR模型的构建目标是最大化后验估计\(p(\Theta \mid >_u )\)，即根据观测数据使得模型参数向最能拟合观测数据的参数的方向移动： \[ p(\Theta \mid >_u ) = \frac{p(>_u \mid \Theta) p(\Theta)}{p(>_u)} \] 其中\(\Theta\)是模型参数，\(>_u\)是已观测到的数据，表示用户\(u\)期望的所有物品的个性化排序，\(p(>_u \mid \Theta)\)是模型预测的用户\(u\)期望排名的概率，\(p(\Theta)\)是参数的先验分布。由于\(p(>_u)\)不依赖于模型参数因此可以视为常数，我们可以简化为： \[ p(\Theta \mid >_u ) \propto p(>_u \mid \Theta) p(\Theta) \] 因此贝叶斯估计可以看作是，在假定\(\Theta\)服从\(p(\Theta)\)的先验分布的情况下，根据观测数据去校正先验分布，矫正项为\(p(>_u \mid \Theta)\)，然后得到后验分布。

我们将最大化后验估计作为个性化排序的目标： \[ \begin{split}\begin{aligned} \textrm{BPR-OPT} : &= \ln p(\Theta \mid >_u) \\ & \propto \ln p(>_u \mid \Theta) p(\Theta) \\ &= \ln \prod_{(u, i, j \in D)} \sigma(\hat{y}_{ui} - \hat{y}_{uj}) p(\Theta) \\ &= \sum_{(u, i, j \in D)} \ln \sigma(\hat{y}_{ui} - \hat{y}_{uj}) + \ln p(\Theta) \\ &= \sum_{(u, i, j \in D)} \ln \sigma(\hat{y}_{ui} - \hat{y}_{uj}) - \lambda_\Theta \|\Theta \|^2 \end{aligned}\end{split} \] 训练集\(D\)定义为\(D \stackrel{\textrm{def}}{=} \{(u, i, j) \mid i \in I^+_u \wedge j \in I \backslash I^+_u \}\)，其中\(I^+_u\)是用户\(u\)的正样本集合，\(I\)表示所有物品，\(I \backslash I^+_u\)表示用户\(u\)的负样本集合。\(\hat{y}_{ui}\)和\(\hat{y}_{uj}\)分别参数为\(\Theta\)的模型预测用户\(u\)对物品\(i\)和\(j\)的偏好得分。\(\sigma\)是\(\text{sigmoid}\)函数，用于将正负样本的得分差异转化为\(0-1\)之间的概率值。先验分布\(p(\Theta)\)是有\(0\)均值和协方差矩阵为\(\Sigma_\Theta\)的多元正态分布（以正态分布初始化模型参数），这里我们令\(\Sigma_\Theta = \lambda_\Theta I\)，因此\(\ln p(\Theta)\)可以转换为\(-\lambda_\Theta \|\Theta \|^2\)，可以看作是对参数的\(L2\)正则化。

理解\(\ln p(\Theta)\)到\(-\lambda_\Theta \|\Theta \|^2\)的转化需要对多元正态分布有一定了解，可以参考《如何直观地理解「协方差矩阵」》

从上述公式可以看出，如果用户的正样本得分高于负样本的差值越大，那么\(\sigma(\hat{y}_{ui} - \hat{y}_{uj})\)越接近1，\(\ln \sigma(\hat{y}_{ui} - \hat{y}_{uj})\)越接近0，最大化BPR-OPT的目标是使得正样本的得分高于负样本的差值尽可能大，下面给出BPRLoss的实现代码：

import torch
from torch import nn
class BPRLoss(nn.Module):
    def __init__(self):
        super(BPRLoss,self).__init__()
    def forward(self,positive,negative):
        distances = positive-negative
        loss = -torch.sum(torch.log(torch.sigmoid(distances)))
        return loss

forward方法接收两个输入参数，分别是单个用户模型预测的正样本得分和负样本得分，然后计算两者的差值，通过torch.sigmoid函数将差值转化为0-1之间的概率值，然后计算torch.log，最后返回损失值。

在实际使用过程中，我们可以通过负采样的方式来生成负样本，即对每个用户的正样本随机采样一个负样本，并将这对正负样本作为一个训练样本，分别输入到模型中计算评分，然后计算BPR损失。下面给出一个简单的例子：

positive = torch.arange(1,10).float()  # 正样本评分
negative = torch.arange(0,9).float()  # 负样本评分
bpr_loss = BPRLoss()
print(bpr_loss(positive,negative), bpr_loss(negative,positive))

1	`tensor(2.8194) tensor(11.8194)`

Hinge损失

Hinge损失是另一种常用的成对损失函数，它的目标是最大化正样本和负样本之间的边界，即使得正样本的得分高于负样本的得分至少一个固定的边界值。Hinge损失的定义如下： \[ \sum_{(u, i, j \in D)} \max( m - \hat{y}_{ui} + \hat{y}_{uj}, 0) \] 其中\(m\)是边界值，\(\hat{y}_{ui}\)和\(\hat{y}_{uj}\)分别是用户\(u\)对物品\(i\)和\(j\)的模型预测得分。当\(m=0\)时，若正样本的得分高于负样本的得分则loss即为0，而当\(m>0\)时，正样本的得分必须高于负样本的得分至少\(m\)才能使得loss为0。这里的\(m\)是一个超参数，用于控制正样本和负样本之间的边界。代码实现如下：

class HingeLoss(nn.Module):
    def __init__(self,margin):
        super(HingeLoss,self).__init__()
        self.margin = margin
    def forward(self,positive,negative):
        distances = self.margin-positive+negative
        loss = -torch.sum(torch.max(distances,torch.zeros_like(distances)))
        return loss

总结

推荐系统中个性化排名任务有三种类型的损失函数，逐点式、成对式和列表式。本文介绍了两种成对式的损失函数，贝叶斯个性化排序损失和Hinge损失，分别用于优化模型参数使得正样本的得分高于负样本的得分。BPR损失是基于最大后验估计推导出来的，而Hinge损失是基于最大化正样本和负样本之间的边界。在实际使用过程中，我们可以根据具体的任务需求选择合适的损失函数。在后面几章我们将使用这两种损失函数来训练模型，以解决推荐系统中的个性化排名任务。

下一章将介绍NeuMF模型，它是结合了矩阵分解模型和多层感知机的混合模型，用于解决推荐系统中的个性化排名任务。