漫游推荐系统（五）—— 用于个性化排名的神经矩阵分解

本文最后更新于 2024年8月19日下午

本章介绍用于隐式反馈建模的神经协同过滤框架（Neural Collaborative Filtering，NCF）。隐式反馈在推荐系统中普遍存在，点击、购买和观看等行为是常见的隐式反馈，这些反馈易于收集且一定程度上反映了用户的偏好。

NeuMF是NCF中的一种，即Neural Matrix Factorization，该模型旨在处理带有隐式反馈的个性化排名任务。该模型利用神经网络的灵活性和非线性来代替矩阵分解的点积。NeuMF模型由两部分组成：多层感知机（MLP）和广义矩阵分解（GMF），这两个子网络的输出被连接起来以计算最后的预测分数。与AutoRec中的评分预测任务不同，NeuMF旨在根据隐式反馈为每个用户生成排名推荐列表，我们将上一节中介绍的个性化排名损失函数来训练该模型。

NeuMF模型

NeuMF模型由两个子网络组成：多层感知机（MLP）和广义矩阵分解（GMF），如下图所示：

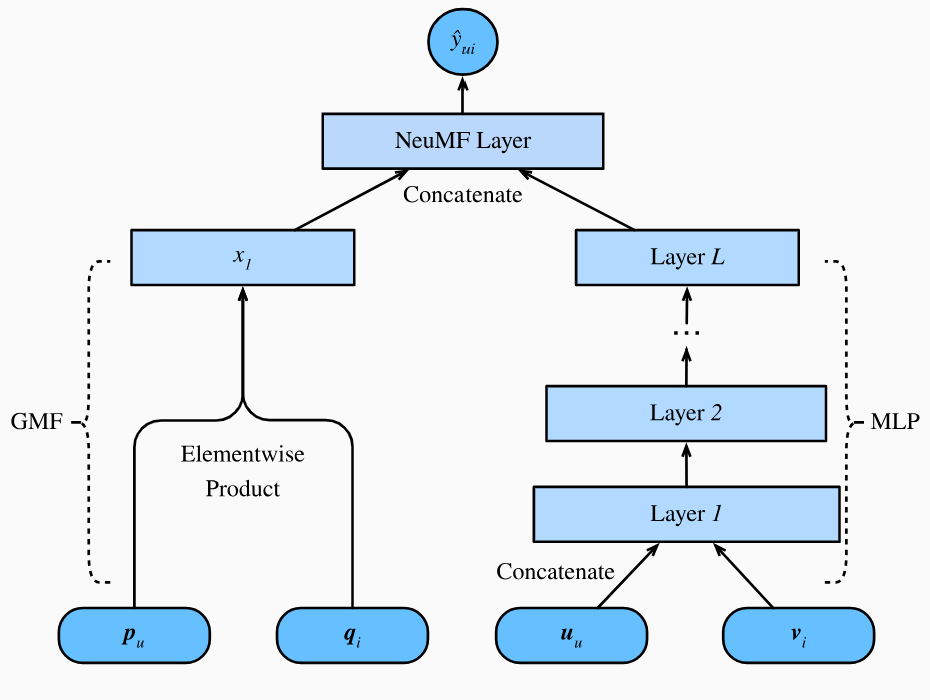
GMF是矩阵分解的神经网络版本，其输入是用户向量和物品向量的Hadamard积（逐元素乘积），模型由两层网络构成： \[ \begin{split}\mathbf{x} = \mathbf{p}_u \odot \mathbf{q}_i \\ \hat{y}_{ui} = \alpha(\mathbf{h}^\top \mathbf{x})\end{split} \] 其中\(x \in \mathbb{R}^k\)是用户向量\(\mathbf{p}_u \in \mathbb{R}^k\)和物品向量\(\mathbf{q}_i \in \mathbb{R}^k\)的逐元素乘积。\(\mathbf{q}_i\)可以理解为物品\(i\)拥有这些特征的程度，是物品嵌入矩阵\(\mathbf{Q} \in \mathbb{R}^{n \times k}\)的第\(i\)行；\(\mathbf{p}_u\)可以理解为用户\(u\)对这些特征的偏好程度，是用户嵌入矩阵\(\mathbf{P} \in \mathbb{R}^{m \times k}\)的第\(u\)行。\(x\)可以理解为用户对这些特征的最后评分。\(\alpha\)是激活函数，\(\mathbf{h} \in \mathbb{R}^k\)是权重向量，\(\hat{y}_{ui}\)是用户\(u\)对物品\(i\)的预测评分。

相较于传统的矩阵分解\(\hat{y}_{ui} = \mathbf{p}_u \mathbf{q}_i^\top\)，GMF不是对\(\mathbf{p}_u \odot \mathbf{q}_i\)直接求和（\(\mathbf{p}_u \mathbf{q}_i^\top\)相当于\(\text{sum}(\mathbf{p}_u \odot \mathbf{q}_i)\)），而是通过一个权重向量\(\mathbf{h}\)来对各个特征得分进行加权，此外，GMF的输出还通过激活函数\(\alpha\)引入非线性变换。

NeuMF模型的另一部分是MLP。为了增强模型的表达能力和灵活性，MLP自网络并没有共享GMF的用户和物品嵌入矩阵，而是又引入了两个独立的用户嵌入矩阵\(\mathbf{U} \in \mathbb{R}^{m \times d}\)和物品嵌入矩阵\(\mathbf{V} \in \mathbb{R}^{n \times d}\)。MLP将用户向量和物品向量拼接后作为输入。通过复杂的连接和非线性变换，MLP子网络能够对用户特征和物品特征之间复杂的交互关系进行建模。MLP子网络定义如下： \[ \begin{split}\begin{aligned} z^{(1)} &= \phi_1(\mathbf{U}_u, \mathbf{V}_i) = \text{concat}\left[ \mathbf{U}_u, \mathbf{V}_i \right] \\ \phi^{(2)}(z^{(1)}) &= \alpha^1(\mathbf{W}^{(2)} z^{(1)} + b^{(2)}) \\ &... \\ \phi^{(L)}(z^{(L-1)}) &= \alpha^L(\mathbf{W}^{(L)} z^{(L-1)} + b^{(L)})) \\ \hat{y}_{ui} &= \alpha(\mathbf{h}^\top\phi^L(z^{(L-1)})) \end{aligned}\end{split} \] 其中\(\mathbf{W}^*, \mathbf{b}^*\)和\(\alpha^*\)分别是第\(l\)层的权重矩阵、偏置向量和激活函数。\(\phi^*\)对应层的函数变换。\(\mathbf{z}^*\)是第\(l\)层的输出向量。

可以看出，GMF和MLP的都能输出用户对物品的评分，一种方式是将两者相加作为最终的预测评分。但是为了更好地融合GMF和MLP，NeuMF模型将GMF和MLP倒数第二层的输出拼接并得到一个特征向量，然后通过一个权重向量\(\mathbf{h}\)来对这个特征向量进行加权，最后通过一个\(\text{sigmoid}\)激活函数来预测得分。最后的预测层定义如下： \[ \hat{y}_{ui} = \sigma(\mathbf{h}^\top[\mathbf{x}, \phi^L(z^{(L-1)})]). \]

模型实现

由于GMF模型和MLP模型不共享嵌入层，因此我们一共需要四个嵌入层。MLP的结构由参数nums_hiddens控制，nums_hiddens是一个列表，其中的每个元素代表MLP每一层的隐藏单元数，激活函数使用\(\text{ReLU}\)：

import torch
from torch import nn

class NeuMF(nn.Module):
    def __init__(self,num_users,num_items,num_factors,num_hiddens,**kwarg):
        super(NeuMF,self).__init__(**kwarg)
        self.P = nn.Embedding(num_users,num_factors)
        self.Q = nn.Embedding(num_items,num_factors)
        self.U = nn.Embedding(num_users,num_factors)
        self.V = nn.Embedding(num_items,num_factors)
        self.mlp = nn.Sequential()
        # in_out记录MLP每一层的输入和输出维度
        self.in_out = [(i,o) for i,o in 
                       zip([2*num_factors]+num_hiddens[:-1],num_hiddens)]
        for i,(in_,out) in enumerate(self.in_out):
            self.mlp.add_module(f'layer_{i}',nn.Linear(in_, out)) 
            self.mlp.add_module(f'activation_{i}',nn.ReLU())
        # num_factors是GMF的输出维度,num_hiddens[-1]是MLP的输出维度
        self.prediction_layer = nn.Linear(num_factors+num_hiddens[-1],1) 
    def forward(self,user_ids,item_ids):
        p_mf = self.P(user_ids)
        q_mf = self.Q(item_ids)
        u_mlp = self.U(user_ids)
        v_mlp = self.V(item_ids)
        gmf = p_mf*q_mf
        mlp = self.mlp(torch.cat([u_mlp,v_mlp],dim=-1))
        # outputs.shape = (batch_size,1)
        outputs = self.prediction_layer(torch.cat([gmf,mlp],dim=-1)) 
        return outputs.squeeze(dim = -1)

使用负采样定制数据集

在前一章我们提到了用成对法构建个性化排名系统，需要对每个正样本随机采样一个负样本，负样本定义为用户没有交互过的物品，也就是未观测到的条目。以下函数接收users和items列表，每行对应用户-物品交互对，同时还接收一个字典candidates，其中键是用户，值是用户交互过的物品列表。可以通过candidates构造一个neg_candidates字典，其中键是用户，值是用户没有交互过的物品列表。neg_candidates字典可以用于负采样，为每一个用户-物品交互对随机采样一个负样本。

在训练阶段，模型确保用户喜欢的项目的排名不高于他不喜欢或没有交互过的项目。

from torch.utils.data import TensorDataset,DataLoader
import random

def generate_PRDatset(users, items, candidates, num_items, device):
    all_items = set(range(num_items))
    neg_candidates = {u: list(all_items - set(cands)) 
                            for u,cands in candidates.items()}
    neg_items = []
    for u in users:
        # 为每个用户随机采样一个负样本
        neg_sample = random.choice(neg_candidates[u])
        neg_items.append(neg_sample)
    users, items, neg_items = (torch.tensor(users).to(device), 
                              torch.tensor(items).to(device), 
                              torch.tensor(neg_items).to(device))
    return TensorDataset(users, items, neg_items)

评估器设计

本节我们将介绍两种用于评估个性化排名模型的评估器，分别是给定排名位置\(\ell\)的命中率（\(\textrm{Hit}@\ell\)）和ROC曲线下的面积（AUC）。\(\textrm{Hit}@\ell\)用于衡量推荐系统是否成功地将用户感兴趣的项目推荐列表的前\(\ell\)个位置，定义如下： \[ \textrm{Hit}@\ell = \frac{1}{m} \sum_{u \in \mathcal{U}} \textbf{1}(rank_{u, g_u} <= \ell) \] 其中\(\textbf{1}\)是指示函数，\(rank_{u, g_u}\)是用户\(u\)的正样本\(g_u\)在推荐列表中的排名，当\(rank_{u, g_u} \leq \ell\)时，\(\textbf{1}(rank_{u, g_u} \leq \ell) = 1\)，否则\(\textbf{1}(rank_{u, g_u} \leq \ell) = 0\)。\(m\)是用户数，\(\mathcal{U}\)是用户集合。

AUC的定义如下： \[ \textrm{AUC} = \frac{1}{m} \sum_{u \in \mathcal{U}} \frac{1}{|\mathcal{I} \backslash S_u|} \sum_{j \in I \backslash S_u} \textbf{1}(rank_{u, g_u} < rank_{u, j}) \] 其中\(\mathcal{I}\)是物品集合，\(S_u\)是用户\(u\)的正样本集合。关于AUC的详细解读可以参考我的另一篇博客《详细解读AUC及其在推荐系统中的应用》，这里不再赘述。

下面的函数用于计算每个用户的\(\textrm{Hit}@\ell\)和AUC，其中items和scores分别是物品和对应的分数，pos_items是用户的正样本集合，k是\(\ell\)的值。函数先根据模型预测分数对物品进行降序排序，并对正负样本进行标记，计算AUC时可以使用sklearn.metrics.roc_auc_score函数，其接收真实标签和预测分数，返回AUC值，我在《详细解读AUC及其在推荐系统中的应用》中介绍了另一种计算AUC的方法，读者有兴趣可以参考。

from sklearn.metrics import roc_auc_score
def hit_and_auc(scores, items, pos_items, k):
    # 根据分数对物品进行降序排序
    ranked_list = sorted(zip(items, scores), reverse=True, key=lambda x: x[1])
    ranked_items = [x[0] for x in ranked_list]
    ranked_scores = [x[1] for x in ranked_list]
    pos_items = set(pos_items)
    # 正样本标签为1，负样本标签为0
    labels = [1 if i in pos_items else 0 for i in ranked_items]
    hit_rate = sum(labels[:k]) / k
    auc = roc_auc_score(labels, ranked_scores)
    return hit_rate, auc

接着使用下面的评估函数对每个用户单独计算\(\textrm{Hit}@\ell\)和AUC，最后返回所有用户的平均值。其中test_candidates是一个字典形式的测试集数据，键是用户，值是用户交互过的物品列表。

def evaluate_ranking(net, test_candidates, num_users, num_items, device):
    hit_rate, auc_list = [], []
    net.eval()
    for u in range(num_users):
        user_ids = [u] * num_items
        item_ids = list(range(num_items))
        scores = []
        user_ids = torch.tensor(user_ids).to(device)
        items = torch.tensor(item_ids).to(device)
        test_data_iter = DataLoader(TensorDataset(user_ids, items), 
                                    batch_size=256, shuffle=False)                            
        # scores是模型预测的用户u与所有物品的评分
        for x in test_data_iter:
            scores.extend(list(net(*x).cpu().numpy()))
        hit,auc = hit_and_auc(scores, item_ids, test_candidates[u], 20)
        hit_rate.append(hit)
        auc_list.append(auc)
    return sum(hit_rate) / len(hit_rate), sum(auc_list) / len(auc_list)

训练与评估模型

由于采用的是成对法构建个性化排名系统，因此需要将正负样本分别输入模型用于预测得分，并输入损失函数用于模型训练。函数定义如下：

from d2l import torch as d2l

def train_ranking(net,train_iter,test_candidates,loss,trainer,
                  num_users,num_items,num_epochs,device,evaluator,eval_step=1):
    hit_rate,auc = 0,0
    net.to(device)
    # 定义动画用于可视化训练过程
    animator = d2l.Animator(xlabel='epoch',xlim=[1,num_epochs],ylim=[0,1],
                            legend=['test hit rate','test AUC'])
    for epoch in range(num_epochs):
        net.train()
        metric,l = d2l.Accumulator(2),0.
        for users, items, neg_items in train_iter:
            # 分别输入正负样本计算得分
            pos_scores = net(users,items)
            neg_scores = net(users,neg_items)
            #梯度清零
            trainer.zero_grad()
            ls = loss(pos_scores,neg_scores)
            ls.backward()
            trainer.step()
            l += ls.item()
            metric.add(l,users.shape[0])
        with torch.no_grad():
            if (epoch+1)%eval_step==0:
                hit_rate,auc = evaluator(
                    net,test_candidates,num_users,num_items,device)
                animator.add(epoch+1,(hit_rate,auc))
    print(f'train loss {metric[0]/metric[1]:.3f}')
    print(f'test hit rate {float(hit_rate):.3f}, test AUC {float(auc):.3f}')

现在我们使用第一章中的MovieLens数据接口加载数据集。由于MovieLens数据集中仅存在评分数据，这里对物品进行评级可以视为隐式反馈的一种形式，因此我们将这些评分二分为1和0，即如果用户对某个物品进行评分，则将隐式反馈视为1，否则视为0，这可以通过设置函数load_data_ml100k中feedback="implicit"实现。训练集和测试集按8:2的比例划分。

batch_size = 256
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
df,num_users,num_items = read_data_ml100k()
# 以'seq-aware'模式划分数据集
train_data,test_data = split_data_ml100k(df,test_ratio=0.2)

# 以隐式反馈模式分别加载训练集和测试集
users_train,items_train,ratings_train,train_candidates = load_data_ml100k(train_data,
                                                num_users,num_items,feedback='implicit')
users_test,items_test,ratings_test,test_candidates = load_data_ml100k(test_data,
                                                num_users,num_items,feedback='implicit')

train_iter = DataLoader(generate_PRDatset(users_train,items_train,train_candidates,num_items,device),
                        batch_size,shuffle=True)

随后创建并初始化模型，设置嵌入层维度为20，并使用三层MLP，每层隐藏单元数为[20,20,20]:

1
2
3

net = NeuMF(num_users, num_items, num_factors=20, num_hiddens=[20, 20, 20])
for param in net.parameters():
    nn.init.normal_(param, mean=0, std=0.01)

训练阶段，使用前一章介绍的BPRLoss损失函数，学习率为0.01，权重衰减率为1e-5，迭代次数为10次，每次评估的间隔为1次：

lr, num_epochs, wd = 0.01, 10, 1e-5
loss = BPRLoss()
trainer = torch.optim.Adam(net.parameters(),lr=lr,weight_decay=wd)
train_ranking(net,train_iter,test_candidates,loss,trainer,num_users,num_items,
                num_epochs,device,evaluate_ranking)

输出如下：

1 2	`train loss 0.134 test hit rate 0.081, test AUC 0.851`

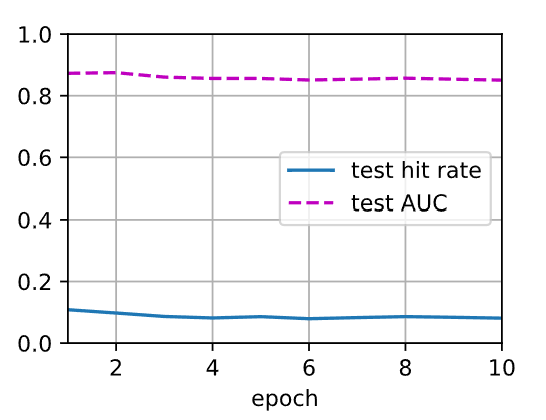
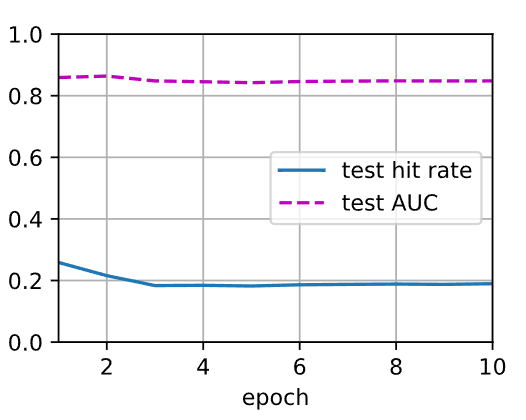
这里test hit rate较低可能是因为测试数据集较小，使得模型预测的前\(\ell\)个物品中正样本的数量较少，我们尝试将训练集和测试集的比例调整为1:1，重新训练模型，输出如下：

1 2	`train loss 0.042 test hit rate 0.190, test AUC 0.848`

小结

本节我们介绍了神经协同过滤模型NeuMF，该模型由GMF和MLP两部分组成，相较于传统的矩阵分解模型，NeuMF引入了非线性变换和复杂的交互关系，能够更好地捕捉用户和物品之间的关系。我们还介绍了如何使用负采样定制数据集，以及两种用于评估个性化排名模型的方法，分别是\(\textrm{Hit}@\ell\)和AUC。最后我们训练了一个NeuMF模型，并在MovieLens数据集上进行了评估。

下一章我们将介绍基于序列感知的个性化推荐模型，该模型能够考略用户的历史行为序列，更好地捕捉用户的兴趣演化过程。