漫游推荐系统（二）—— 矩阵分解

本文最后更新于 2024年8月16日 晚上

矩阵分解（Matrix Factorization）是一种在推荐系统中被广泛认可和使用的技术。MF模型的一个版本是由Simon Funk在其博客Netflix Update: Try this at home中提出的，他在文中描述了分解交互矩阵的方法。在本节中，我们将深入探讨矩阵分解模型及其实现的细节。

矩阵分解模型

矩阵分解模型是一类协同过滤模型。模型通过将用户-物品交互矩阵分解为两个低秩矩阵的乘积，从而学习用户和物品的隐向量表示。

令\(\mathbf{R} \in \mathbb{R}^{m \times n}\)表示用户-物品交互矩阵，\(m\)和\(n\)分别表示用户和物品的数量。矩阵\(\mathbf{R}\)中的元素\(\mathbf{R}_{ui}\)表示用户\(u\)对物品\(i\)的评分。矩阵分解模型将交互矩阵\(\mathbf{R}\)分解为两个低秩矩阵\(\mathbf{P} \in \mathbb{R}^{m \times k}\)和\(\mathbf{Q} \in \mathbb{R}^{n \times k}\)的乘积，其中\(k\)表示隐向量的维度且\(k \ll m, n\)。令\(\mathbf{p}_u\)表示矩阵\(\mathbf{P}\)的第\(u\)行，\(\mathbf{q}_i\)表示矩阵\(\mathbf{Q}\)的第\(i\)行。对于给定的物品\(i\)，\(\mathbf{q}_i\)向量中的每个元素可以理解为该物品拥有这些特征的程度，对于给定的用户\(u\)，\(\mathbf{p}_u\)向量中的每个元素可以理解为用户\(u\)对这些特征的喜好程度。用户\(u\)对物品\(i\)的评分\(\hat{\mathbf{R}}_{ui}\)可以通过两个向量的内积计算得到： \[ \hat{\mathbf{R}}_{ui} = \mathbf{p}_u \mathbf{q}_i^{\top} \] 整体的预测评分矩阵\(\hat{\mathbf{R}}\)可以通过矩阵\(\mathbf{P}\)和\(\mathbf{Q}\)的乘积估算得到，如下图所示： \[ \hat{\mathbf{R}} = \mathbf{P} \mathbf{Q}^{\top} \]

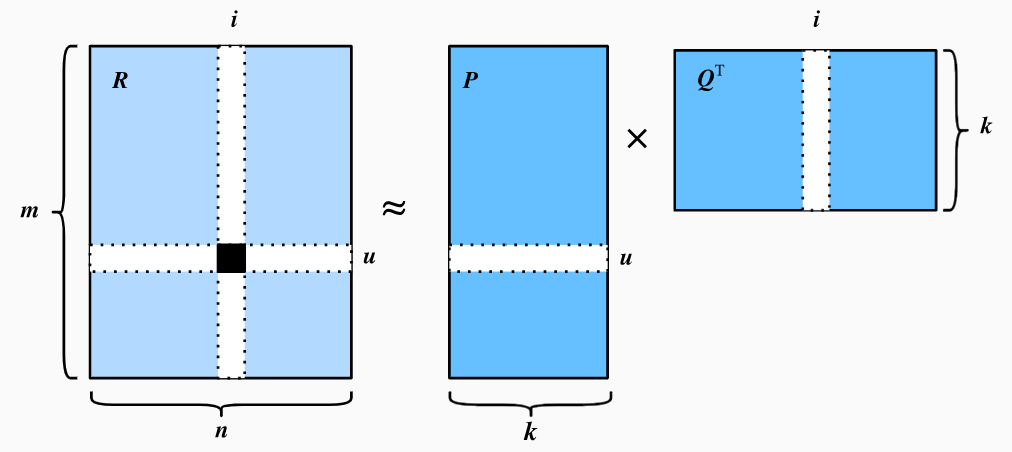
其中\(\hat{\mathbf{R}} \in \mathbb{R}^{m \times n}\)是预测的评分矩阵并且有着与\(\mathbf{R}\)相同的维度。在上述建模中我们还忽略了一个问题，即无法对用户或物品的偏差建模，这里的“偏差”指的是用户或物品的评分倾向性。例如，有些用户倾向于给出较高的评分，而有些物品可能因为质量较差总是得到较低的评分。这种偏差在现实世界的应用中是常见的，即用户和物品的评分行为可能受到个人偏好或物品固有特性的影响。

为了捕捉这些偏差，可以引入针对用户和物品的偏差项\(b_u\)和\(b_i\)。这意味着在计算预测评分时会考虑每个用户和物品的独立性。例如对于倾向于给出较高的评分的用户其偏差项可能会较大，而对于质量较差的物品其偏差项可能会较小。因此，预测评分的计算公式可以修改为： \[ \hat{\mathbf{R}}_{ui} = \mathbf{p}_u \mathbf{q}_i^{\top} + b_u + b_i \] 随后我们可以通过最小化预测评分与真实评分之间的误差来学习模型参数，常用的损失函数是均方误差（Mean Squared Error, MSE），目标函数如下： \[ \underset{\mathbf{P}, \mathbf{Q}, b}{\mathrm{argmin}} \sum_{(u, i) \in \mathcal{K}} \| \mathbf{R}_{ui} - \hat{\mathbf{R}}_{ui} \|^2 + \lambda (\| \mathbf{P} \|^2_F + \| \mathbf{Q} \|^2_F + b_u^2 + b_i^2 ) \] 其中\(\mathcal{K}\)是训练集中用户-物品交互矩阵\(\mathbf{R}\)中的非空元素集合，即\(\mathcal{K} = \{ (u, i) | \mathbf{R}_{ui} \text{ is known} \}\)，这样可以避免对未知评分（默认为0）的样本进行训练。同时引入正则项\(\lambda (\| \mathbf{P} \|^2_F + \| \mathbf{Q} \|^2_F + b_u^2 + b_i^2 )\)来惩罚参数的大小，避免过拟合，这一步也被称为权重衰减（Weight Decay），其中\(\lambda\)是正则化系数，我们可以通过在优化器中设置weight_decay参数来实现，而不需要在损失函数中显式添加正则项。

在后面几节，我们将通过实现矩阵分解模型并在MovieLens数据集上进行训练和评估，MovieLens数据集的数据接口已经在在漫游推荐系统（一）——概述中实现了。

我们先导入所需的库和模块。

1
2
3
4
5
import torch
import torch.nn as nn
import torch.optim as optim
import pandas as pd
from d2l import torch as d2l

模型实现

对于用户和物品的隐向量，我们可以通过nn.Embedding模块来实现，输入维度为用户或物品的数量，输出维度为隐向量的维度。同时我们还需要定义用户和物品的偏差项，同样可以通过nn.Embedding模块来实现，输出维度为1。在模型的前向计算中，用户和物品的ids会作为输入，通过nn.Embedding模块得到用户和物品的隐向量，然后计算预测评分。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class MF(nn.Module):
    def __init__(self,num_factors,num_users,num_items,**kwargs):
        super(MF,self).__init__(**kwargs)
        self.P = nn.Embedding(num_users,num_factors)
        self.Q = nn.Embedding(num_items,num_factors)
        self.user_bias = nn.Embedding(num_users,1)
        self.item_bias = nn.Embedding(num_items,1)
    def forward(self,user_id,item_id):
        
        """
        Forward pass of the recommender system model.

        Args:
            user_id (torch.Tensor): Tensor containing user IDs, shape: (batch_size,).
            item_id (torch.Tensor): Tensor containing item IDs. shape: (batch_size,).

        Returns:
            torch.Tensor: Tensor containing the predicted outputs. shape: (batch_size,).
        """
            
        P = self.P(user_id) # shape: (batch_size, num_factors)
        Q = self.Q(item_id) # shape: (batch_size, num_factors)
        b_u = self.user_bias(user_id)
        b_i = self.item_bias(item_id)
        # b_u和b_i的shape为(batch_size,1),suqeeze去掉最后一维
        outputs = (P*Q).sum(axis=1)+torch.squeeze(b_u)+torch.squeeze(b_i)
        return outputs

评估方法

我们使用均方根误差（Root Mean Squared Error, RMSE）来评估模型的性能，这种方法通常用于预测分数与真实分数之间的差异。\(RMSE\)是\(MSE\)的平方根，计算公式如下： \[ \textrm{RMSE} = \sqrt{\frac{1}{|\mathcal{T}|}\sum_{(u, i) \in \mathcal{T}}(\mathbf{R}_{ui} -\hat{\mathbf{R}}_{ui})^2} \] 其中\(\mathcal{T}\)是测试集，\(|\mathcal{T}|\)是测试集中的样本数量。我们可以使用nn.MSELoss来计算均方误差，然后取平方根得到均方根误差。 

1
2
3
4
5
6
7
8
9
10
def evaluator(net,test_iter):
    net.eval()
    mse = torch.nn.MSELoss()
    rmse_list = []
    for users,items,ratings in test_iter:
        predicts = net(users,items) # shape: (batch_size,)
        rmse = torch.sqrt(mse(predicts,ratings))
        rmse_list.append(rmse.item())
    mean_rmse = sum(rmse_list)/len(rmse_list)
    return mean_rmse

训练与评估

在训练步骤，我们使用权重衰减（weight decay）来对模型参数进行正则化，这和我们在目标函数中添加正则项是等价的: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def train_recsys_rating(net,train_iter,test_iter,loss,trainer,
                        num_epochs,device,evaluator,**kwargs):
    # 设置一个训练曲线动画
    animatior = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs], 
                             ylim=[0, 2], legend=['train loss', 'test rmse'])
    net.to(device)
    for epoch in range(num_epochs):
        net.train()
        l = 0.
        for users,items,ratings in train_iter:
            trainer.zero_grad()
            predicts = net(users,items)
            ls = loss(predicts,ratings)
            ls.backward()
            trainer.step()
            l += ls.item()      
        with torch.no_grad():
            test_rmse = evaluator(net, test_iter)
        train_l = l/len(train_iter)
        animatior.add(epoch+1,(train_l,test_rmse))
        print(f'train loss {train_l:.3f}, test rmse {test_rmse:.3f}')
最后我们将所有模块组合在一起，然后在MovieLens数据集上训练和评估模型。 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
lr, num_epochs, wd = 0.002, 20, 1e-5
num_users, num_items, train_iter, test_iter = split_and_load_ml100k(
    											split_mode='seq_aware', 
                                                feedback='explicit', 
                                                test_ratio=0.1, 
                                                batch_size=256, 
                                                device=device)
net = MF(10,num_users,num_items)
for param in net.parameters():
    nn.init.normal_(param,mean=0,std=0.01) # 初始化参数
loss = nn.MSELoss() # 使用均方误差作为损失函数
trainer = optim.Adam(net.parameters(),lr,weight_decay=wd) # 使用Adam优化器,设置weight_decay参数
train_recsys_rating(net,train_iter,test_iter,loss,trainer,num_epochs,device,evaluator)
最后一次输出： 
1
train loss 0.663, test rmse 0.915
模型的训练和评估结果如下图所示：

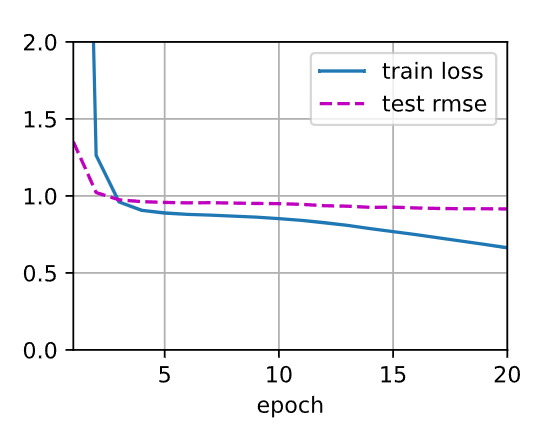
最后我们来使用训练好的模型来预测测试集前五个条目的评分，并与真实的评分对比： 

1
2
3
4
5
6
7
8
9
10
users,items,scores = None,None,None
# 获取测试集的前5个条目
for u,i,r in test_iter:
    users,items,scores = u[:5],i[:5],r[:5]
    break
predicts = net(users,items)
print(pd.DataFrame({'user_id':users.cpu().numpy(),
                    'item_id':items.cpu().numpy(),
                    'real score':scores.cpu().numpy(),
                    'predict score':predicts.cpu().detach().numpy()}))
输出如下： 
1
2
3
4
5
6
   user_id  item_id  real score  predict score
0   623   	125         4.0       3.547791
1   180  	1136        1.0       1.687140
2   849   	479         5.0       4.105268
3   446   	283         4.0       2.944871
4   368   	357         3.0       3.134766

小结

在本节中，我们实现了矩阵分解模型，并在MovieLens数据集上进行了训练和评估。通过学习用户和物品的隐向量表示，模型可以预测用户对物品的评分。下一章我们将介绍AutoRec模型，它是一个基于自动编码器的推荐系统模型。

微信二维码

微信支付

支付宝二维码

支付宝支付

推荐系统
#推荐系统
漫游推荐系统（二）—— 矩阵分解
https://qinyu.space/推荐系统/漫游推荐系统（二）——矩阵分解/
作者
QinYU
发布于
2024年8月16日
许可协议