漫游推荐系统（三）—— AutoRec

本文最后更新于 2024年8月17日 凌晨

在上一节我们介绍了矩阵分解MF模型，虽然MF能够在一些评分预测模型上取得不错的效果，但其本质上还是一个线性模型，因此这类模型缺乏捕捉用户和物品之间的复杂交互关系的能力，而这些非线性关系可能对预测用户偏好有很大的帮助。

本节我们将介绍一个非线性的协同扩散模型AutoRec，它是基于自动编码器（Autoencoder）的推荐模型，但是和传统的自动编码器有所不同。

一方面，AutorRec模型有着与自动编码器相同的结构，包括一个输入层，一个隐层和一个重建层（输出层）。自动编码器的目标是学习如何将输入数据复制到输出，同时将输入数据编码成隐藏层的低维表示，比如BERT模型就是一个自动编码器，通过Masked Language Model任务来学习文本的嵌入表示。

另一方面，AutoRec模型并不将用户或物品嵌入到低维空间中，而是直接将交互矩阵的行或列作为输入，然后在输出层重构输入的交互矩阵。因此AutoRec不需要像矩阵分解模型那样需要学习用户和物品低维特征向量，而是学习输入层到隐层的映射关系和隐层到输出层的映射关系。

AutoRec有两种变体，分别是基于用户的AutoRec和基于物品的AutoRec，它们的区别在于输入层是用户还是物品的交互矩阵。在这里我们以基于物品的AutoRec为例，介绍其的模型结构和训练方法，基于用户的AutoRec与基于用户的AutoRec类似，读者可以看完本章后自行推导。

模型结构

令\(\mathbf{R}_{*i} \in \mathbb{R}^{m}\)表示评分矩阵的第\(i\)列，即物品\(i\)的评分向量，\(m\)表示用户的数量，\(\mathbf{R}_{*i}\)中每个元素表示一个用户对物品\(i\)的评分，如果用户没有对物品\(i\)评分，则对应的元素为0。模型的架构定义如下： \[ h(\mathbf{R}_{*i}) = f(\mathbf{W} \cdot g(\mathbf{V} \mathbf{R}_{*i} + \mu) + b) \] 其中\(f(\cdot)\)和\(g(\cdot)\)是激活函数，\(\mathbf{V} \in \mathbb{R}^{d \times m}\)是输入层到隐层的映射矩阵，\(\mathbf{W} \in \mathbb{R}^{m \times d}\)是隐层到输出层的映射矩阵，\(\mu\)和\(b\)分别是输入层和隐层的偏置向量。\(h( \cdot )\)表示整个AutoRec模型。

模型会先将物品的评分向量\(\mathbf{R}_{*i}\)压缩到一个低维的隐层表示，然后再重建物品的评分向量。这个过程中，模型关注的是物品的特征表示，因此这是一个item-based的模型。

那么这样编码再解码有什么意义呢？

物品的评分向量通常是稀疏的，即大部分用户没有对特定物品进行评分。通过编码过程，模型学习到一个低维的特征表示，这个表示可以被认为是物品的“浓缩”版本，包含了关于该物品最重要的信息。解码器则利用这个隐层表示尝试重建完整的评分向量，这相当于模型在尝试预测缺失的评分，从而缓解稀疏矩阵问题。

因此输入层到隐层的映射矩阵\(\mathbf{V} \in \mathbb{R}^{d \times m}\)可以看成模型从物品的评分向量中提取物品的特征表示，特征向量的维度\(d\)通常小于用户的数量\(m\)，而隐层到输出层的映射矩阵\(\mathbf{W} \in \mathbb{R}^{m \times d}\)的每一行向量可以视为单个用户对\(d\)个特征的加权权重，即用户对物品特征的偏好，最后加权求和得到用户对物品的评分。这种构建方式与矩阵分解模型实际上有着一定的相似性。

在矩阵分解中我们定义用户特征矩阵\(\mathbf{P} \in \mathbb{R}^{m \times d}\)和物品特征矩阵\(\mathbf{Q} \in \mathbb{R}^{n \times d}\)，通过\(\hat{\mathbf{R}} = \mathbf{P} \mathbf{Q}^{\top}\)预估评分。在AutoRec中，我们可以将\(\mathbf{W} \in \mathbb{R}^{m \times d}\)视为\(\mathbf{P}\)，将\((\mathbf{V} \mathbf{R})^{\top} \in \mathbb{R}^{n \times d}\)视为\(\mathbf{Q}\)，只不过矩阵分解模型中的\(\mathbf{P}\)和\(\mathbf{Q}\)是通过定义嵌入层得到的，而AutoRec中\((\mathbf{V} \mathbf{R})^{\top}\)是将评分矩阵通过隐层映射得到的。更为重要的是，AutoRec中使用了非线性激活函数，这使得模型可以学习到更为复杂的用户和物品之间的交互关系。

我们使用下面目标函数来最小化重构误差，同时引入L2正则化项来惩罚模型的较大权重： \[ \underset{\mathbf{W},\mathbf{V},\mu, b}{\mathrm{argmin}} \sum_{i=1}^M{\parallel \mathbf{R}_{*i} - h(\mathbf{R}_{*i})\parallel_{\mathcal{O}}^2} +\lambda(\| \mathbf{W} \|_F^2 + \| \mathbf{V}\|_F^2) \]

其中\(\| \cdot \|_{\mathcal{O}}\)表示只考虑训练集中已有评分的损失，即考虑预测结果中已有评分的位置，而不考虑未评分的损失，因此在反向传播时只有与观察到的输入值相关联的权重会被更新。

在实现模型之前我们先导入一些必要的库： 

1
2
3
4
5
import torch
import torch.nn as nn
import torch.optim as optim
import pandas as pd
from d2l import torch as d2l

模型实现

典型的自动编码器由编码器和解码器组成，编码器将输入数据映射到低维表示，解码器将低维表示映射回原始数据。我们使用两个全连接层作为编码器和解码器，编码器权重为\(\mathbf{V} \in \mathbb{R}^{d \times m}\)，解码器权重为\(\mathbf{W} \in \mathbb{R}^{m \times d}\)。我们使用\(\text{sigmoid}\)作为编码器的激活函数，并在编码后使用dropout来防止过拟合。在前向传播阶段，如果处于训练模式，我们使用torch.sign函数筛选出已知评分的位置，然后只输入这些位置的预测评分用于计算损失；在评估阶段，我们则输出所有位置的预测评分。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class AutoRec(nn.Module):
    def __init__(self,num_users,num_hidden,dropout=0.05,**kwargs):
        super(AutoRec,self).__init__(**kwargs)
        self.encoder = nn.Linear(num_users,num_hidden)
        self.sigmoid = nn.Sigmoid()
        self.dropout = nn.Dropout(dropout)
        self.decoder = nn.Linear(num_hidden,num_users)
    def forward(self,input):
        # input.shape: (batch_size, num_users)
        # hidden.shape: (batch_size, num_hidden)
        hidden = self.dropout(self.sigmoid(self.encoder(input)))
        pred = self.decoder(hidden)
        # mask the gradient for the missing values duiring training
        if self.training:
            return pred*torch.sign(input)
        else:
            return pred

评估器设计

由于输入变为了物品的评分向量，我们需要重新设计评估器。这里需要注意test_iter中同时包含了训练集物品评分向量和测试集物品评分向量，我们将train_scores输入到模型中获得填补了缺失值的预测评分，然后使用torch.sign函数筛选出测试集中已知评分的位置，计算\(RMSE\)时只考虑这些位置的预测评分。 

1
2
3
4
5
6
7
8
9
10
11
12
13
def evaluator(net, test_iter):
    net.eval()
    rmse_list = []
    for test_scores, train_scores in test_iter:
        # input.shape: (batch_size, num_users)
        predict = net(train_scores)
        # filter将测试集中的缺失项的预测值过滤掉
        filter = torch.sign(test_scores)
        # 使用L2范数计算RMSE，需要除以filter.sum()来确保仅考虑测试集中有评分的项
        rmse = torch.sqrt(torch.sum(torch.square(
            predict * filter - test_scores)) / torch.sum(filter)).item()
        rmse_list.append(rmse)
    return sum(rmse_list)/len(rmse_list)

注意评估时不能将test_scores作为模型的输入，因为模型是在训练集的评分向量上训练的，目的是让模型通过以观测的数据来预测缺失值，而train_scores和test_scores评分分布可能不同，将test_scores输入到模型中会得到不准确的预测结果。

训练与评估

我们仍使用MovieLens数据集来训练和评估模型，数据接口在第一章中已经介绍过，这里不再赘述。我们定义训练函数如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def train_recsys_rating(net,train_iter,test_iter,loss,trainer,
                        num_epochs,device,evaluator,**kwargs):
    # 设置一个训练曲线动画
    animatior = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs], 
                             ylim=[0, 2], legend=['train loss', 'test rmse'])
    net.to(device)
    for epoch in range(num_epochs):
        net.train()
        l = 0.
        for (items_scores,) in train_iter:
            trainer.zero_grad()
            predicts = net(items_scores)
            ls = loss(predicts,items_scores)
            ls.backward()
            trainer.step()
            l += ls.item()      
        with torch.no_grad():
            test_rmse = evaluator(net, test_iter)
        train_l = l/len(train_iter)
        animatior.add(epoch+1,(train_l,test_rmse))
        print(f'train loss {train_l:.3f}, test rmse {test_rmse:.3f}')

接下来我们加载数据并训练模型，注意这里和第二章不同，我们使用交互评分矩阵作为输入，而不是user，item，rating的三元组。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Load the MovieLens 100K dataset
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
df, num_users, num_items = read_data_ml100k()
train_data, test_data = split_data_ml100k(df, num_users, num_items)
# train_inter_mat.shape: (num_items, num_users)
# test_inter_mat.shape: (num_items, num_users)
_, _, _, train_inter_mat = load_data_ml100k(train_data, num_users, num_items)
_, _, _, test_inter_mat = load_data_ml100k(test_data, num_users, num_items)

train_data = TensorDataset(train_inter_mat.to(device))
# test_data包含了训练集和测试集的物品评分向量
test_data = TensorDataset(test_inter_mat.to(device),
                          train_inter_mat.to(device))
train_iter = DataLoader(train_data, batch_size=256, shuffle=True)
test_iter = DataLoader(test_data, batch_size=256)

# Model initialization, training, and evaluation
net = AutoRec(num_users, num_hidden=300)
for param in net.parameters():
    nn.init.normal_(param, mean=0, std=0.01)
lr, num_epochs, wd = 0.01, 25, 1e-5
loss = nn.MSELoss()
trainer = optim.Adam(net.parameters(), lr=lr, weight_decay=wd)
train_recsys_rating(net, train_iter, test_iter, loss,
                    trainer, num_epochs, device, evaluator)

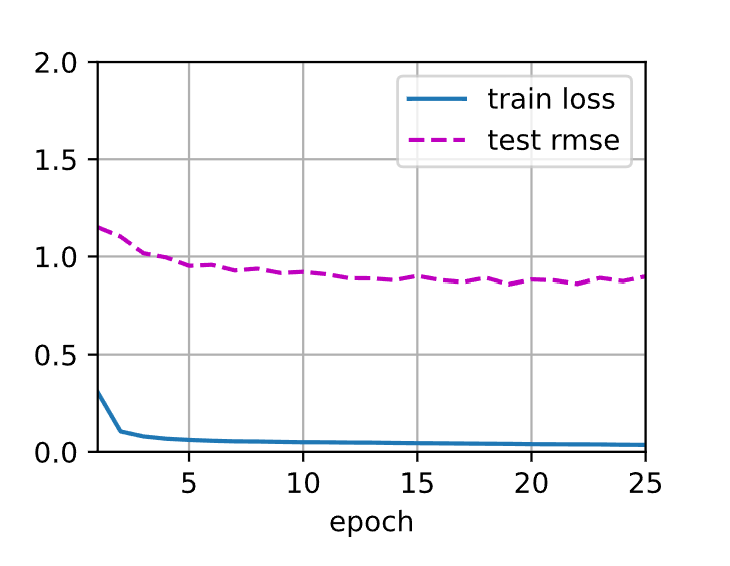
输出如下，测试集上的RMSE损失要低于矩阵分解模型得到的结果，并且训练速度要远快于矩阵分解模型。

1
train loss 0.036, test rmse 0.899

小结

AutoRec是一个基于自动编码器的推荐模型，它通过编码器将物品的评分向量映射到低维表示，然后再通过解码器重构物品的评分向量，以此来预测评分矩阵中的缺失值。相较于矩阵分解模型，AutoRec模型引入了非线性激活函数，可以学习到更为复杂的用户和物品之间的交互关系。

下一章我们将介绍一些会在排名系统中使用的损失函数。

微信二维码

微信支付

支付宝二维码

支付宝支付

推荐系统
#推荐系统
漫游推荐系统（三）—— AutoRec
https://qinyu.space/推荐系统/漫游推荐系统（三）——AutoRec/
作者
QinYU
发布于
2024年8月17日
许可协议